cho \(\Delta ABC\left(AB\ne AC\right)\). E,F lần lượt là chân đường vuông góc kẻ từ B, C đến đường phân giác AD.K là giao điểm của FB và CE.
CMR: AK là đường phân giác ngoài của \(\Delta ABC\)tại đỉnh A.
cho tam giác ABC(ab khác ac).Gọi E,F theo thứ tự là các hình chiếu của B,C trên tia phân giác của góc A. Gọi K là giao điểm của các đường thẳng FB và CE.CMR AK là tia phân giác của góc ngoài đỉnh A
Cho tam giác ABC. Gọi E và F là chân các đường vuông góc kẻ từ đỉnh A xuống đến các phân giác trong và phân giác ngoài của góc B. Gọi H và K lần lượt là chân cá đường vuông góc kẻ từ đỉnh A xuống các đường phân giác trong và phân giác ngoài của góc C.
Tam giác ABC phải có đặc điểm gì để tứ giác AEBF và AHCK bằng nhau? Mọi người chia 2 trường hợp nghen
2 truong hop nhu nhau ma.
TH1 neu AE=CH,BE=AH
Ap dung dinh li py ta go ta co
Do AEB la tam giac vuong
=> AB2=AE2+BE2(1)
Do AHC la tam giac vuong
=> AC2=AH2+HC2(2)
Ma AE=CH,BE=AH(3)
Từ 1 2 3 => AB=AC
Th 2: AE=AH,BE=CH lam tt
Bạn tự cm tứ giác AEBF và tứ giác AHCK là hcn nhe
Cho \(\Delta ABC\) các đường phân giác của các góc ngoài tại B và C cắt nhau ở E .
Gọi G,H,K theo thứ tự là chân đường vuông góc .Kẻ từ E đến BC,AB,AC
a) Có nhận xét gì về độ dài EH,EG,EK
b) CM: AE là tia phân giác góc BAC
c) Đường phân giác của góc ngoài tại A của \(\Delta ABC\)cắt BE,CE tại D,F . CM: \(EA\perp DF\)
d) Các đường AE,BF,CD là đường gì trong \(\Delta ABC\)
e) Các đường EA,FB,DC là đường gì trong \(\Delta DEF\)
Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB (h.81). Chứng minh rằng ba điểm D, E, F năm trên cùng một đường tròn có tâm K.
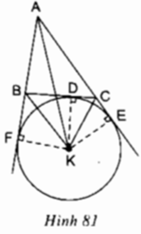
Theo tính chất tia phân giác, ta có:
AK là tia phân giác của góc BAC
⇒ KE = KF
Tương tự: CK là tia phân giác của góc ngoài của góc ACB
⇒ KE = KD
Do đó: KE = KF = KD
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm K
cho tam giác ABC , phân giác ngoài tại B và C cắt nhau tại E . Gọi G,H,K thứ tự là chân đường vuông góc kẻ từ E đến các đường thẳng BC,AB,AC. đường phân giác ngoài tại A của tam giác ABC cắt các đường thẳng BE,CE tại D,F.
a,các đường thẳng AE,BF,CD là các đường gì trong tam giác ABC
b, các đường thẳng EA ,FB ,DC là các đường gì trong tam giác DEF
Cho tam giác ABC Các đường phân giác của các góc ngoài đỉnh B và đỉnh C cắt nhau ở E gọi G H K theo thứ tự là chân đường vuông góc kẻ từ A đến các đoàn BC AB AC
a) có nhận xét gì về độ dài các đoạn EH EG EK
b) Chứng minh AE là tia phân giác của góc B AC
c) đường phân giác góc ngoài đỉnh A của tam giác ABC cắt các đường thẳng BE CE tại D và F Chứng minh AE vuông góc với DF
d các đường thẳng AE BF CD là các đường gì trong tam giác ABC
e các đường thẳng AE FB CD là các đường gì trong tam giác DEF
a) E thuộc tia phân giác của \(\widehat{CBH}\)
\(\Rightarrow\)EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của \(\widehat{BCK}\)
\(\Rightarrow\)EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
\(\Rightarrow\)E thuộc tia phân giác của \(\widehat{BAC}\)mà E khác A
Vậy AE là tia phân giác của \(\widehat{BAC}\)
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
\(\Rightarrow AE\perp AF\) (tính chất hai góc kề bù)
Hay \(AE\perp DF\)
d) Chứng minh tương tự câu a ta có BF là tia phân giác của \(\widehat{ABC}\)
CD là tia phân giác của \(\widehat{ACB}\)
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
\(\Rightarrow BF\perp BE\) (tính chất hai góc kề bù)
Hay \(BF\perp ED\)
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
\(\Rightarrow CD\perp CE\)(tính chất hai góc kề bù)
Hay \(CD\perp EF\)
Các đường thẳng AE, FB, DC là các đường cao trong tam giác DEF.
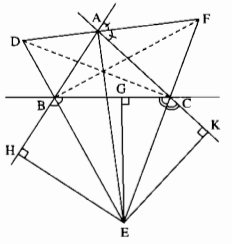
Cho tam giác ABC, các đường phân giác của các góc ngoài tại B và C cắt nhau ở E. Gọi G, H, K theo thứ tự là chân đường vuông góc kẻ từ E đến các đường thẳng BC, AB, AC. Đường phân giác của góc ngoài tại A của tam giác ABC cắt các đường thẳng BE, CE tại D, F. Chứng minh rằng EA vuông góc với DF.
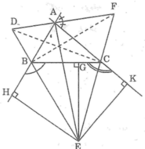
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
Cho tam giác ABC (AB 6= AC). Gọi E và F theo thứ tự là các hình chiếu
của B và C trên tia phân giác của góc A. Gọi K là giao điểm của các đường thẳng
FB và CE. Chứng minh rằng AK là tia phân giác của góc ngoài tại đỉnh A của tam
giác ABC.
1)Tam giác ABC vuông cân tại A, đường trung tuyến AM. Gọi D là điểm thuộc đoạn thẳng MC. Gọi H là chân đường vuông góc kẻ từ B đến AD. Gọi I, K lần lượt là chân đường vuông góc kẻ từ M đến AD và BH. Chứng minh HM là tia phân giác của góc BHD.
2)Tam giác ABC có I là giao điểm các tia phân giác của các góc B và C. Gọi d là giao điểm của AI và BC. Kẻ IH vuông góc với BC( H thuộc BC). Chứng minh rằng góc BIH= góc CID.
3) Cho tam giác ABC có góc C=30 độ. Tia phân giác của góc B và đường phân giác của góc ngoài tại A cắt nhau ở E. Tính số đo góc BCE.
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
Bài làm
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau:
5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2.
Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7
Ta làm như sau: 6 - 7
Không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5.
Vậy 8,6 - 2,7 = 5,9