Theo tính chất tia phân giác, ta có:
AK là tia phân giác của góc BAC
⇒ KE = KF
Tương tự: CK là tia phân giác của góc ngoài của góc ACB
⇒ KE = KD
Do đó: KE = KF = KD
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm K
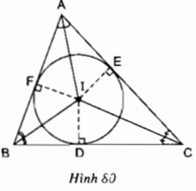
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.
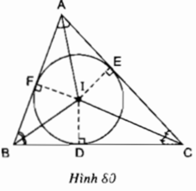
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).
1. Cho tam giác ABC nhọn, vẽ đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự tại D,E
a) Chứng minh:CD vuông góc AB; BE vuông góc AC.
b)Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC.
2. Cho tam giác ABC( góc A > 90 độ) . Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh:
a) A,D,B,E cùng thuộc một đường tròn.
b) A,D,C,F cùng thuộc một đường tròn.
c) B,C,E,F cùng thuộc một đường tròn .
1. Cho tam giác ABC nhọn, vẽ đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự tại D,E
a) Chứng minh:CD vuông góc AB; BE vuông góc AC.
b)Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC.
2. Cho tam giác ABC( góc A > 90 độ) . Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh:
a) A,D,B,E cùng thuộc một đường tròn.
b) A,D,C,F cùng thuộc một đường tròn.
c) B,C,E,F cùng thuộc một đường tròn .
1. Cho tam giác ABC nhọn, vẽ đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự tại D,E
a) Chứng minh:CD vuông góc AB; BE vuông góc AC.
b)Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC.
2. Cho tam giác ABC( góc A > 90 độ) . Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh:
a) A,D,B,E cùng thuộc một đường tròn.
b) A,D,C,F cùng thuộc một đường tròn.
c) B,C,E,F cùng thuộc một đường tròn .
1. Cho tam giác ABC nhọn, vẽ đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự tại D,E
a) Chứng minh:CD vuông góc AB; BE vuông góc AC.
b)Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC.
2. Cho tam giác ABC( góc A > 90 độ) . Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh:
a) A,D,B,E cùng thuộc một đường tròn.
b) A,D,C,F cùng thuộc một đường tròn.
c) B,C,E,F cùng thuộc một đường tròn .
1. Cho tam giác ABC nhọn, vẽ đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự tại D,E
a) Chứng minh:CD vuông góc AB; BE vuông góc AC.
b)Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC.
2. Cho tam giác ABC( góc A > 90 độ) . Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh:
a) A,D,B,E cùng thuộc một đường tròn.
b) A,D,C,F cùng thuộc một đường tròn.
c) B,C,E,F cùng thuộc một đường tròn .
1. Cho tam giác ABC nhọn, vẽ đường tròn đường kính BC cắt các cạnh AB,AC theo thứ tự tại D,E
a) Chứng minh:CD vuông góc AB; BE vuông góc AC.
b)Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc BC.
2. Cho tam giác ABC( góc A > 90 độ) . Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh:
a) A,D,B,E cùng thuộc một đường tròn.
b) A,D,C,F cùng thuộc một đường tròn.
c) B,C,E,F cùng thuộc một đường tròn .
