Câu hỏi
# Cho dãy tỉ số bằng nhau ( 2bz-3cy )/a=(3cx az)/2b=(ay-2bx)/3c. Chứng minh: x/a=y/2b=z/3c.
Trả lời
Đáp án:+Giải thích các bước giải:


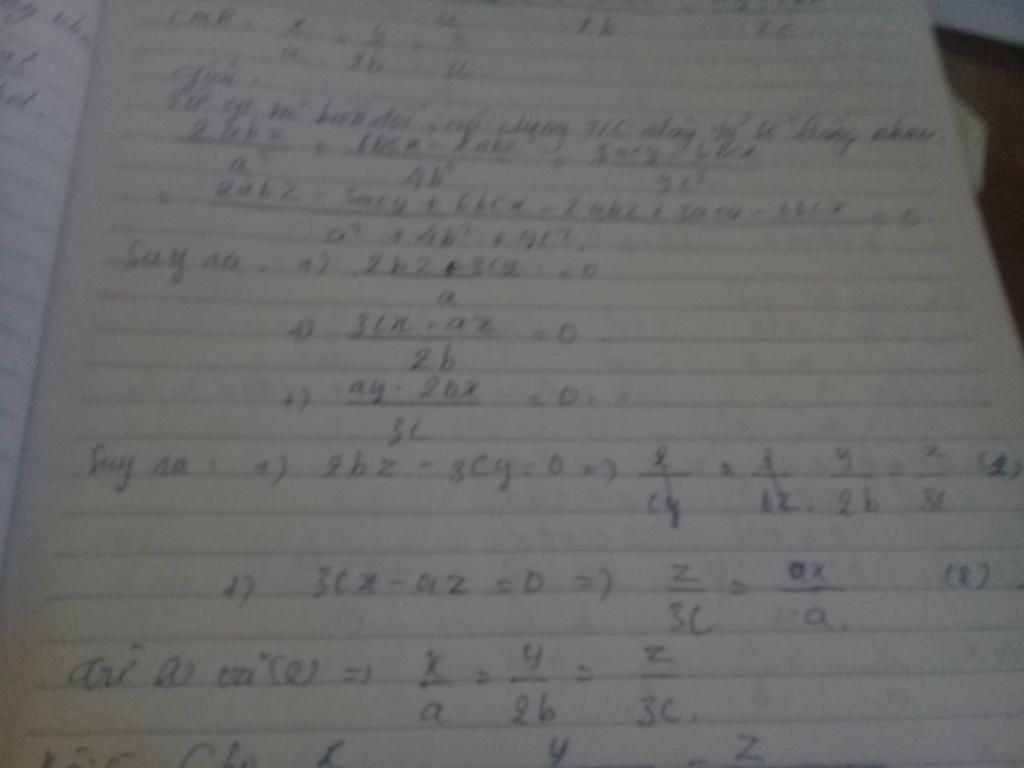
bạn tìm trên link này nhá mk ko gửi hình ảnh đc

Theo đề: \(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}\)

\(\Rightarrow\frac{2bza-3acy}{a^2}=\frac{6cxb-2bza}{4b^2}=\frac{3ayc-6bxc}{9c^2}\)

\(=\frac{2bza-3cya+6xbc-2bza+3ayc-6bxc}{a^2+4b^2+9c^2}\)

\(=0\)

\(\Rightarrow\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}=0\)

\(\Rightarrow2bz=3cy;3cx=az;ay=2bx\)

\(\Rightarrow\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}\left(đpcm\right)\)

Ta có: \(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}\)

\(\Rightarrow\frac{2bzx-3cyx}{ax}=\frac{3cxy-azy}{2by}=\frac{ayz-2bxz}{3xz}\)

\(=\frac{2bzx-3cyx-3cxy-azy-ayz-2bxz}{ax-2by-3xz}=0\)

\(\Rightarrow\)\(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}=0\)

\(\Rightarrow2bz=3cy;\)\(3cx=az;\)\(ay=2bx\)

\(\Rightarrow\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}\).

\(\dfrac{2bz-3cy}{a}=\dfrac{3cx-az}{2b}=\dfrac{ay-2bx}{3c}\\ \Rightarrow\dfrac{2abz-3acy}{a}=\dfrac{6bcx-2abz}{2b}=\dfrac{3acy-6bcx}{3c}\\ =\dfrac{\left(2abz-3acy\right)+\left(6bcx-2abz\right)+\left(3acy-6bcx\right)}{a+2b+3c}\\ =\dfrac{\left(2abz-2abz\right)+\left(3acy-3acy\right)+\left(6bcx-6bcx\right)}{a+2b+3c}=0\\ \)

\(\Rightarrow2bz-3cy=3cx-az=ay-2bx=0\\ \Rightarrow\left\{{}\begin{matrix}2bz=3cy\\3cx=az\\ay=2bx\end{matrix}\right.\)

\(2bz=3cy\Rightarrow\dfrac{2b}{y}=\dfrac{3c}{z}\\ 3cx=az\Rightarrow\dfrac{3c}{z}=\dfrac{a}{x}\\ ay=2bx\Rightarrow\dfrac{a}{x}=\dfrac{2b}{y}\\ \Rightarrow\dfrac{a}{x}=\dfrac{2b}{y}=\dfrac{3c}{z}\Rightarrow.....\)

dễ mà

t thì chẳng thấy dễ chút nào nhưng t làm dc

Ta thấy a, b, c \(\ne\) 0 nên a² + (2b)² + (3c)² \(\ne\) 0.

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}=\frac{2abz-3cay}{a^2}=\frac{6bcx-2abz}{\left(2b\right)^2}=\frac{3cay-6bcx}{\left(3c\right)^2}\)
\(=\frac{2abz-3cay+6bcx-2abz+3cay-6bcx}{a^2+\left(2b\right)^2+\left(3c\right)^2}\) (Do a² + (2b)² + (3c)² \(\ne\) 0)
\(=\frac{0}{a^2+\left(2b\right)^2+\left(3c\right)^2}=0\)

\(\Rightarrow\left\{{}\begin{matrix}2bz=3cy\\3cx=az\\ay=2bx\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\frac{y}{2b}=\frac{z}{3c}\\\frac{z}{3c}=\frac{x}{a}\\\frac{x}{a}=\frac{y}{2b}\end{matrix}\right.\)

\(\Rightarrow\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}\)

\(\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}\)

Suy ra: \(\frac{a.\left(2bz-3cy\right)}{a.a}=\frac{2b\left(3cx-az\right)}{2b.2b}=\frac{3c.\left(ay-2bx\right)}{3c.3c}\)

\(\Rightarrow\frac{2abz-3acy}{a^2}=\frac{3bcx-abz}{2b^2}=\frac{acy-2cbx}{3c^2}\)

Theo tính chất dãy tỉ số bằng nhau

\(\frac{2abz-3acy+6bcx-2abz+3acy-6bcx}{a^2+2b^2+3c^2}=\frac{0}{a^2+2b^2+3c^2}=0\)

\(\Rightarrow\hept{\begin{cases}2bz=3cy\\3cx=az\\ay=2bx\end{cases}\Rightarrow\hept{\begin{cases}\frac{z}{3c}=\frac{y}{2b}\\\frac{x}{a}=\frac{z}{3c}\\\frac{y}{2b}=\frac{x}{a}\end{cases}}\Rightarrow\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}}\)

=> đpcm