cho hình thang cân ABCD (AB// CD). có AB =15cm, CD= 25cm: DB là tia phân giác góc D. Tính gần đúng 68% diện tích hình thang ABCD
giúp tui với :((
Những câu hỏi liên quan
Cho hình thang cân ABCD(AB // CD) có AB = 15cm,CD = 25cm ;DB là tia phân giác góc D.tính gần đúng 68% diện tích hình thang ABCD
Cho hình thang ABCD(AB // CD).M,N lần lượt là trung điểm AD và BC. MN cắt BD,AC theo thức tự ở I và K. Tính độ dài IK biết AB= 10,26cm và CD=22,4cm
Đúng 0
Bình luận (0)
Cho hình thang cân ACD(AB//CD) AB=15cm, CD=25cm. DB là phân giác góc D. Tính 68% diện tích ABCD?
Xét tg ABD, ta có:
^ABD = ^BDC (so le trong)
^BDC = ^ADB (gt)
=> ^ABD = ^ADB
=> tg ABD cân tại A => AD=AB = 15cm
Kẻ đường cao AH của hình thang cân
=> BH = (CD-AB)/2 = 5cm (bạn c/m điểm này nghe)
=> AH2 = AD2 - BH2 = 200
=> AH = 14,14
=> S(ABCD) = AH.(AB+CD)/2 =282,8
=> 68% diện tích ABCD = 192,3 cm2
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//DC) biết AB =15cm, DC=25cm. Biết BD là tia phân giác của góc D. Tính gần đúng 65% diện tích hình thang
Cho hình thang ABCD có AB//CD, AB<CD, đường chéo BD vuông góc với cạnh BC. Kẻ BH vuông góc với CD. Tính diện tích hình thang ABCD biết BC=15cm, DC= 25cm. (ABCD ko phải hình thang cân)
Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên BC và đồng thời DB là tia phân giác của
A
D
C
^
.
a) Tính các góc của hình thang cân ABCD.b) Biết BC 6 cm, tính chu vi và diện tích của hình thang cân ABCD
Đọc tiếp
Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên BC và đồng thời DB là tia phân giác của A D C ^ .
a) Tính các góc của hình thang cân ABCD.
b) Biết BC = 6 cm, tính chu vi và diện tích của hình thang cân ABCD
a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2
Đúng 0
Bình luận (0)
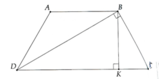
Cho hình thang ABCD cân (AB//CD) có DB là tia phân giác góc D,DB +BC ,B+AB= 4cm .tính chu vi hình thang
Cho hình thang cân ABCD (AB//CD) có đường chéo BD vuông góc với cạnh bên BC và đồng thời DB là tia phân giác của góc ADC
a) Tính các góc của hình thang cân ABCD
b) Biết BC=42cm. Tính chu vi và diện tích của hình thang ABCD
Nhận cày thuê điểm hỏi đáp nha...
Quan tâm ib mình!!
Đúng 0
Bình luận (0)
hình thang cân ABCD ( AB //CD ) có DB là tia phân giác của góc D , DB vuông góc BC. Biết AB = 10 cm, CD=24 cm . tính chu vi hình thang
hình thang cân ABCD ( AB //CD ) có DB là tia phân giác của góc D , DB vuông góc BC. Biết AB = 4 cm . tính chu vi hình thang
\(\widehat{ABD}=\widehat{BDC}\left(SLT\right);\widehat{ADB}=\widehat{BDC}\left(GT\right)\\ \Rightarrow\widehat{ABD}=\widehat{ADB}\Rightarrow AD=AB=BC=4\left(cm\right)\)
(tam giác \(ADB\) cân tại \(A\))
Vì là h.thang cân mà có: BD là phân giác \(\widehat{D}\) nên AC cũng là phân giác \(\widehat{C}\) \(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
Dễ thấy các góc bằng nhau: \(\widehat{BAC}=\widehat{ADB}=\widehat{BDC}=\widehat{ACD}=\widehat{ACB}=\widehat{ABD};\widehat{DBC}=\widehat{DAC}=90\)
\(\Rightarrow6\widehat{BDC}+90+90=360\Rightarrow\widehat{BDC}=30\)
\(\sin\widehat{BDC}=\dfrac{BC}{DC}\Rightarrow DC=\dfrac{BC}{\sin\widehat{BDC}}=\dfrac{4}{\sin30}=8\left(cm\right)\)
\(\Rightarrow P_{ABCD}=4+4+8+4=20\left(cm\right)\)
Đúng 4
Bình luận (3)
Vì AB // DC => góc ABD = góc BDC
Mà góc ADB = góc BDC ( DB là phân giác ADC )
=> góc ABD = góc ADB
=> tam giác ADB cân tại A
=> AD = AB = 4 (cm)
Mà ABCD là hình thang cân
=> AD = BC = 4 (cm)
Có : góc BDC = 1/2 góc ADC
mà góc ADC = góc BCD ( ABCD là hình thang cân )
=> góc BDC = 1/2 góc BCD => góc BCD = 2 . BDC
Xét tam giác BCD vuông tại B có
BDC + BCD = 90
<=> BDC + 2BDC = 90
<=> BDC = 30
mà BC là cạnh đối diện góc BDC
=> BC = 1/2 BD
Hay 4 = 1/2 BD
=> BD = 8 (cm)
Áp dụng ĐL Pytago vào tam giác BDC vuông tại B được
BC2 + DC2 = BD2
<=> DC = \(\sqrt{BD^2-BC^2}\)
<=> DC= \(\sqrt{8^2-4^2}=4\sqrt{3}\)
Vậy chu vi hình thang ABCD là
AB + BC + CD + AD = 4 + 4 + 4\(\sqrt{3}\) + 4 =12 + 4\(\sqrt{3}\) ( cm )
Đúng 1
Bình luận (0)