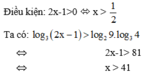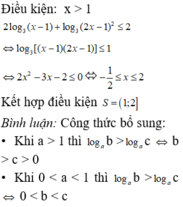Giải bất phương trình : log32x>1

Những câu hỏi liên quan
Giải các bất phương trình: log 3 2 x - 5 log 3 x + 6 ≤ 0
Điều kiện: x > 0.
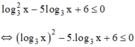
(Bất phương trình bậc hai ẩn log3x).
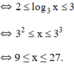
Vậy bất phương trình có tập nghiệm [9; 27].
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
log
3
2
x
-
3
1
-
x
1
A. B. C. D.
Đọc tiếp
Tập nghiệm của bất phương trình log 3 2 x - 3 1 - x < 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tập nghiệm của bất phương trình
log
3
2
x
−
1
4
là: A.
65
2
;
+
∞
B.
1
2
;
41
C. ...
Đọc tiếp
Tập nghiệm của bất phương trình log 3 2 x − 1 > 4 là:
A. 65 2 ; + ∞
B. 1 2 ; 41
C. 41 ; + ∞
D. − ∞ ; 41
Đáp án C
Do cơ số lớn hơn 1 nên BPT tương đương
2 x − 1 > 3 4 = 81 ⇔ 2 x > 82 ⇔ x > 41
Đúng 0
Bình luận (0)
Nghiệm của bất phương trình
log
3
2
x
-
1
log
2
9
.
log
3
4
là. A. x 41 B.
x
1
2
C.
x
65
2
D.
1
2...
Đọc tiếp
Nghiệm của bất phương trình log 3 2 x - 1 > log 2 9 . log 3 4 là.
A. x > 41
B. x > 1 2
C. x > 65 2
D. 1 2 < x < 65 2
Tập nghiệm của bất phương trình:
2
log
3
x
-
1
+
log
3
2
x
-
1
≤
2
là: A.
S
1
;
2
B.
S
-
1...
Đọc tiếp
Tập nghiệm của bất phương trình: 2 log 3 x - 1 + log 3 2 x - 1 ≤ 2 là:
A. S = 1 ; 2
B. S = - 1 2 ; 2
C. 1 ; 2
D. S = ( 1 ; 2 ]
Tập nghiệm của bất phương trình
log
3
2
x
-
3
1
-
x
1
là A.
1
x
≤
4
3
B.
x
5
6
C. ...
Đọc tiếp
Tập nghiệm của bất phương trình log 3 2 x - 3 1 - x < 1 là
A. 1 < x ≤ 4 3
B. x > 5 6
C. 6 5 < x < 4 3
D. 6 5 < x ≤ 4 3
Đáp án D
Điều kiện
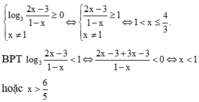
Kết hợp với điều kiện nghiệm của bất phương trình là 6 5 < x ≤ 4 3
Đúng 0
Bình luận (0)
Tìm tập nghiệm S của bất phương trình
log
1
2
(
log
3
2
x
+
1
x
-
1
)
0
A.
S
(
-
∞
,
1...
Đọc tiếp
Tìm tập nghiệm S của bất phương trình log 1 2 ( log 3 2 x + 1 x - 1 ) > 0
A. S = ( - ∞ , 1 ) ∪ ( 4 ; + ∞ )
B. S = ( - ∞ ; - 2 ) ∪ ( 1 ; + ∞ )
C. (-2; 1) ∪ (1; 4)
D. S = ( - ∞ ; - 2 ) ∪ ( 4 ; + ∞ )
Giải các bất phương trình sau:a) (2x − 7)ln(x + 1) 0;b) (x − 5)(logx + 1) 0;c) 2
log
3
2
x
+ 5
log
2
2
x
+
log
2
x
– 2 ≥ 0d) ln(3
e
x
− 2) ≤ 2x
Đọc tiếp
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
a) Bất phương trình đã cho tương đương với hệ sau:
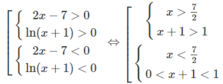
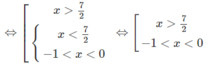
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
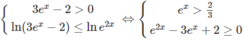
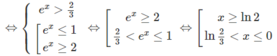
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
Đúng 0
Bình luận (0)
Giải phương trình
log
3
2
x
-
1
-
1
2
Đọc tiếp
Giải phương trình log 3 2 x - 1 = - 1 2
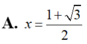
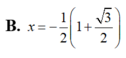
![]()
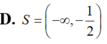
Cho phương trình
log
3
2
x
+
log
3
2
x
+
1
-
2
m
-
1
0
. Tập tất cả các giá trị của tham số m để phương trình có nghiệm thuộc đoạn
1
;
3
3
là A.
0
≤
m
≤...
Đọc tiếp
Cho phương trình log 3 2 x + log 3 2 x + 1 - 2 m - 1 = 0 . Tập tất cả các giá trị của tham số m để phương trình có nghiệm thuộc đoạn 1 ; 3 3 là
A. 0 ≤ m ≤ 1
B. 0 ≤ m ≤ 2
C. 0 ≤ m ≤ 13 6
D. 1 ≤ m ≤ 2
Điều kiện: x > 0
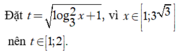
Phương trình trở thành
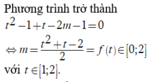
Do đó yêu cầu bài toán ![]()
Chọn B.
Đúng 0
Bình luận (0)