cho tam giác ABC. E là trung điểm hoặc I là trung điểm của AE . Gọi M là giao điểm BI và AC.K là trung điểm của MC a) Chứng minh IM = 1/2 EK b) Chứng minh AM = CK ( giup em voi )

Những câu hỏi liên quan
cho tam giác ABC. E là trung điểm hoặc I là trung điểm của AE . Gọi M là giao điểm BI và AC.K là trung điểm của MC a) Chứng minh IM = 1/2 EK b) Chứng minh AM = CK (giup em voi )
a: Xét ΔBMC có
E là trung điểm của BC
K là trung điểm của MC
Do đó: KE là đường trung bình của ΔBMC
Suy ra: KE//IM
Xét ΔAEK có
I là trung điểm của AM
IM//EK
Do đó: M là trung điểm của AK
Xét ΔAEK có
I là trung điểm của AM
M là trung điểm của AK
Do đó: IM là đường trung bình của ΔAEK
Suy ra: \(IM=\dfrac{1}{2}KE\)
b: Ta có: AM=MK
MK=KC
Do đó: AM=CK
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB AC. M là trung điểm BC.a) Chứng minh: tam giác MAB tam giác MACb) Chừng minh AM là tia phân giác của góc BAC và AM vuông góc BCc) Lấy điểm E trên AB, điểm F trên AC sao cho AE AF. Gọi G là trung điểm EF. Chứng minh: 3 điểm A; G; M thẳng hàng.d) Chứng minh: EF // BCe) Trên tia EF lấy K sao cho EK BC. Gọi I là giao điểm của BC và EK. Chứng minh: I vừa là trung điểm của EC vừa là trung điểm của BK
Đọc tiếp
Cho tam giác ABC có AB = AC. M là trung điểm BC.
a) Chứng minh: tam giác MAB = tam giác MAC
b) Chừng minh AM là tia phân giác của góc BAC và AM vuông góc BC
c) Lấy điểm E trên AB, điểm F trên AC sao cho AE = AF. Gọi G là trung điểm EF. Chứng minh: 3 điểm A; G; M thẳng hàng.
d) Chứng minh: EF // BC
e) Trên tia EF lấy K sao cho EK = BC. Gọi I là giao điểm của BC và EK. Chứng minh: I vừa là trung điểm của EC vừa là trung điểm của BK
Giải
a) vì m la trung diểm của BC => BM=MC
Xét tam giac BAM va tam giac MAC có:
AB=AC(dề bài cho)
BM=MC(Chung minh tren)
AM la cạnh chung(de bai cho)
=>Tam giác BAM=tam giac MAC(c.c.c)
b)từ trên
=>góc BAM=góc MAC(hai goc tuong ung)
Tia AM nam giua goc BAC (1)
goc BAM=goc MAC(2)
từ (1) va (2)
=>AM la tia phan giac cua goc BAC
c)Còn nữa ......-->
Đúng 0
Bình luận (0)
B)vi goc BAM =90 độ
MAC=90 độ
=>AM vuông góc voi BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I. a) Chứng minh rằng AD// BM và tứ giác ADBM là hình thoi. b) Gọi E là giao điểm của AM và AD. Chứng minh AE = EM
a: Xét tứ giác ADBM có
I là trung điểm của AB
I là trung điểm của DM
Do đó: ADBM là hình bình hành
mà AM=BM
nên ADBM là hình thoi
Đúng 0
Bình luận (0)
cho tam giác ABC có AB=AC. Gọi M là trung điểm của cạnh BC. a)Chúng minh: tam giác ABM= tam giác ACM b)Chứng minh: AM vuông góc với BC c)Gọi I là trung điểm của đoạn thẳng AM. Qua A kẻ đường thẳng d vuông góc với A. Gọi E là giao điểm của đường thẳng của d và tia BI. Chứng minh AE=Bm d)Gọi K là trung điểm của AC. Chứng minh ba điểm M,K,E thẳng hàng
*Tự vẽ hình
a) Xét tam giác ABM và ACM, có :
AB=AC(GT)
AM-cạnh chung
BM=MC(GT)
-> Tam giác ABM=ACM(c.c.c)
b) Do tam giác ABM=ACM (cmt)
-> \(\widehat{AMB}=\widehat{AMC}=90^o\)
-> AM vuông góc BC
c) Xét tam giác AEI và MBI, có :
\(\widehat{EAI}=\widehat{BMI}=90^o\)
\(\widehat{AIE}=\widehat{BIM}\left(đđ\right)\)
AI=IM(GT)
-> tam giác AEI=MBI(g.c.g)
-> AE=BM ( đccm)
d) Chịu. Tự làm nhe -_-'
#Hoctot
bạn tự vẽ hình
a, xét tam giác ABM và tam giác ACM có :
AB=AC (gt)
MB=MC (gt)
AM là cạch chung
suy ra tam giác ABM =tam giác ACN (c.c.c)
b, Vì tam giác ABM = tam giác ACN (câu a)
suy ra góc M1= góc M2 (2 góc tương ứng)
mà M1+M2=180 ( 2 góc kề bù)
suy ra : M1=M2= 90
suy ra AM vuông góc BC
c, Vì tam giác ABM = tam giác ACM (câu a)
suy ra : A1=A2 ( 2 góc tương ứng)
suy ra: AM là phân giác góc BAC
minh cung chiu phan d ne
Cho am giác ABC vuông cân tại A, M là trung điểm của canh BC , E là điểm nằm giữa M và C . Vẽ BH vuông góc AE, CK vuông góc AE
a,Chứng minh BH=AK
b, Chứng minh tam giác MHK vuông cân
c, Gọi I là trung điểm AH. Chứng minh IM vuông góc BK
a) Ta có : ^BAK+^KAC=90 độ (1)
^HBA+^BAH ( hay ^BAK)=90 độ (2)
Từ (1) và (2)=> ^KAC=^HBA ( vì đều bằng 90 độ - ^BAK )
Xét 🔺BHA và 🔺AKC có :
^BHA = ^AKC = 90 độ
AB=AC ( vì 🔺ABC vuông cân ở A )
^KAC = ^HBA ( chứng minh trên )
Suy ra 🔺BHA = 🔺AKC ( cạnh huyền - góc nhọn )
=> BH = AK ( 2 góc tương ứng )
b, ΔMBH = ΔMAK:
Ta có: BH ⊥ AK; CK ⊥ AE.
=> BH // CK.
=> HBMˆ=MCKˆHBM^=MCK^ (2 góc so le trong) [1]
Mà MAEˆ+AEMˆ=90oMAE^+AEM^=90o [2]
Và MCKˆ+CEKˆ=90oMCK^+CEK^=90o [3]
AEMˆ=CEKˆAEM^=CEK^ (đối đỉnh) [4]
Từ [1], [2], [3] và [4] => MAEˆ=ECKˆMAE^=ECK^ [5]
Từ [1] và [5] => HBMˆ=MAKˆHBM^=MAK^.
Ta có: AM là trung tuyến của tam giác vuông ABC nên AM = BM = MC = 1212BC.
Xét ΔMBH và ΔMAK có:
+ MA = MB (cmt)
+ HBMˆ=MAKˆHBM^=MAK^ (cmt)
+ BH = AK (câu a)
=> ΔMBH = ΔMAK (c - g - c)
c, ΔMHK vuông cân:
Xét ΔAMH và ΔCMK có:
+ AH = CK (ΔABH = ΔCAK)
+ MH = MK (ΔMBH = ΔMAK)
+ AM = CM (AM là trung tuyến)
=> ΔAMH = ΔCMK (c - c - c)
=> AMHˆ=CMKˆAMH^=CMK^ (2 góc tương ứng)
mà AMHˆ+HMCˆ=90oAMH^+HMC^=90o
=> CMKˆ+HMCˆ=90oCMK^+HMC^=90o
hay HMKˆ=90oHMK^=90o.
ΔHMK có MK = MH và MHKˆ=90oMHK^=90o.
=> ΔHMK vuông cân tại M.
con 💖*•.¸♡ ₷ℴá¡↭ℳųộ¡↭2ƙ7 ♡¸.•*mày copy thôi chứ
ở đây cấm coppy lúc nào z m
Xem thêm câu trả lời
Cho tam giác ABC trung tuyến AM (M thuộc BC) có I là trung điểm của AM. Tia BI cắt AC tại D. Gọi E là trung điểm của DC.
a) Chứng minh ME = \(\dfrac{1}{2}\) BD
b) Chứng minh D là trung điểm của AE.
c) Chứng minh BD = 4ID.
a: Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của DC
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//BD và \(ME=\dfrac{1}{2}BD\)
b: Xét ΔAME có
I là trung điểm của AM
ID//ME
Do đó: D là trung điểm của AE
Đúng 1
Bình luận (0)
Cho tam giác ABC đường trung tuyến AM . Gọi K là trung điểm của AM . Kẻ CK cắt AB tại E.Gọi F là trung điểm của BE chứng minh : a) EK // FM b) AE = EF = BF (giúp em với )
a: Xét ΔBEC có
M là trung điểm của BC
F là trung điểm của BE
Do đó: MF là đường trung bình của ΔBEC
Suy ra: MF//EC
hay EK//FM
b: Xét ΔAFM có
K là trung điểm của AM
KE//FM
Do đó: E là trung điểm của FA
Suy ra: EA=FE=FB
Đúng 1
Bình luận (0)
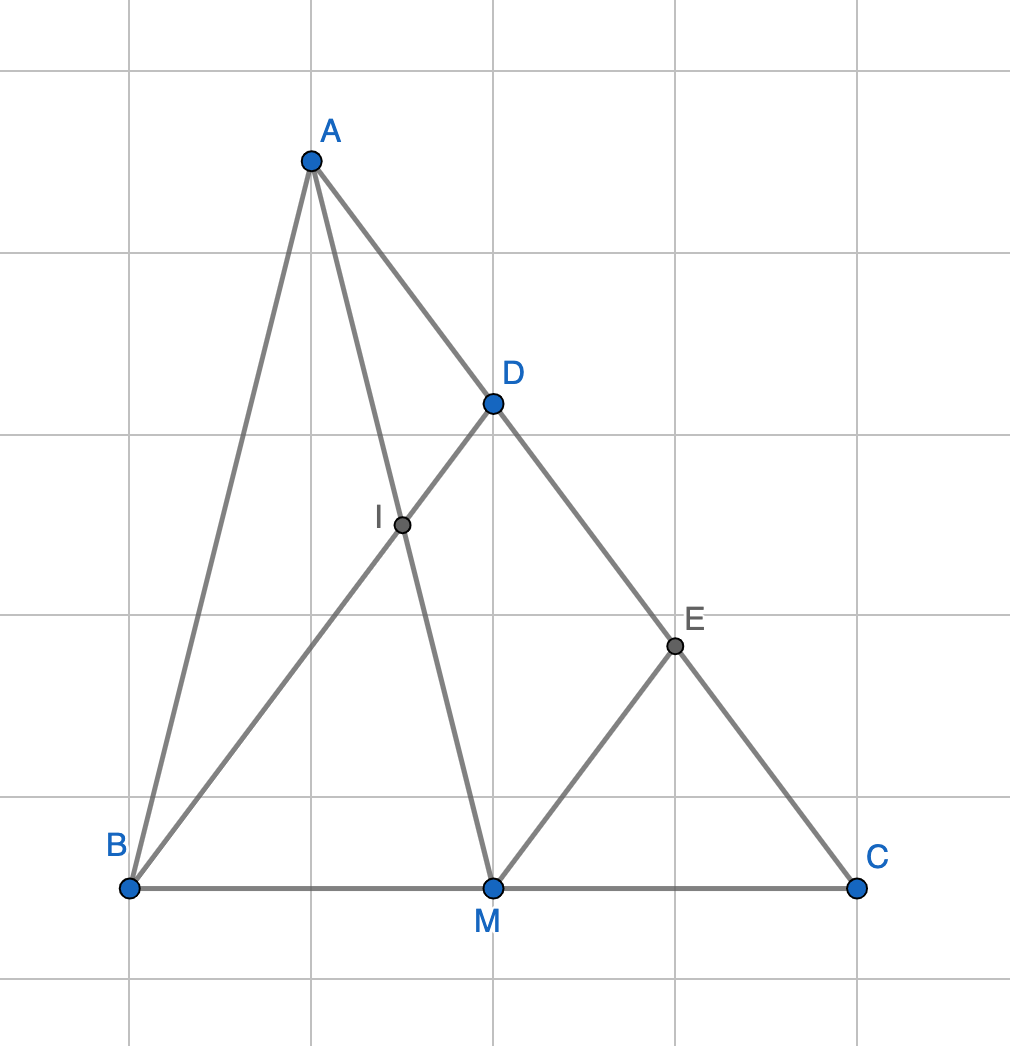
Cho tam giác ABC, trung tuyến AM . Lấy D trên AC sao cho DA= \(\dfrac{1}{2}\)DC .Gọi I là giao điểm của AM và DB , gọi E là trung điểm DC
a, chứng minh AD=DE=EC
b, Chứng minh DEMB là hình thang
C, Chứng minh IA=IM
a) Ta có: \(AD=\dfrac{1}{2}DC\)(gt)
mà \(EC=ED=\dfrac{DC}{2}\)(E là trung điểm của DC)
nên AD=EC=ED
b) Xét ΔCDB có
M là trung điểm của BC(gt)
E là trung điểm của CD(gt)
Do đó: ME là đường trung bình của ΔCDB(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//BD và \(ME=\dfrac{1}{2}BD\)(Định lí 2 về đường trung bình của tam giác)
hay ME//ID
Xét tứ giác MEDB có ME//BD(cmt)
nên MEDB là hình thang có hai đáy là ME và BD(Định nghĩa hình thang)
c) Xét ΔAME có
D là trung điểm của AE(AD=DE, D nằm giữa A và E)
DI//ME(cmt)
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
hay IA=IM(Đpcm)
Đúng 2
Bình luận (0)
\(a.\) Ta có: DA=\(^{\dfrac{1}{2}DC=DE=EC}\) (đpcm)
\(b.\) Xét tam giác DBC có:
\(\left\{{}\begin{matrix}DE=CE\\BM=CM\end{matrix}\right.\) \(\Rightarrow\) ME là đường trung bình tam giacs DBC
\(\Rightarrow ME\)//\(BD\) \(\Rightarrow\) DEMB là hình thang
\(c.\)Vì \(\Rightarrow ME\)//\(BD\) nên ME // ID
Xét tam giác AMD có: \(\left\{{}\begin{matrix}ME\backslash\backslash ID\\AD=DC\end{matrix}\right.\)
=> ME là đường trung bình tam giác AMD hay I là trung điểm MA
\(\Rightarrow IA=IM\) (đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc vưông tại a có ab>ac gọi m là trung điểm bc từ m kẻ md vuông góc vớii ab tại d và me vuông góc với ac tại e
a) chứng minh adme là hcn
b) gọi f là điểm đối xứng với m qua e chứng minh tứ giác amcf là hình thoi
c) gọi ik lần lượt là trung điểm của bc và mc .chứng minh bi +ek bằng am
d)gọi n là giao điểm của am và be chứng minh af=3mn




















