Từ một điểm M cố định nằm ngoài đường tron (O), kẻ tiếp tuyến MA và cát tuyến MBC.CMR tích MA.MB không đổi

Những câu hỏi liên quan
Từ một điểm M cố định ở bên ngoài đường tròn (O), kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. Chứng minh rằng luôn có M T 2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
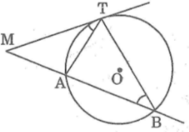

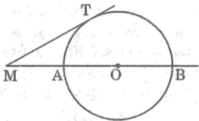
Vì cát tuyến MAB kẻ tùy ý nên ta luôn có M T 2 = MA.MB không phụ thuộc vị trí của cát tuyến MAB.
Đúng 0
Bình luận (0)
Cho đường tròn (O) một điểm M cố định không nằm trên đường tròn, qua M kẻ cát tuyến cắt (O) tại A và B. CMR tích MA.MB không đổi
Giải
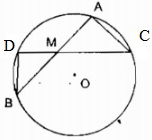
Trường hợp M ở bên trong đường tròn (O)
Kẻ cát tuyến AB bất kỳ và kẻ đường thẳng MO cắt đường tròn tại C và D.
Xét hai ∆MAC và ∆MBD:
ˆAMC=ˆBMDAMC^=BMD^ (đối đỉnh)
ˆA=ˆDA^=D^ (hai góc nội tiếp cùng chắn cung BCBC⏜
Suy ra: ∆MAC đồng dạng ∆MDB (g.g)
⇒MBMC=MDMA⇒MBMC=MDMA
⇒MA.MB=MC.MD⇒MA.MB=MC.MD (1)
Vì M, O cố định suy ra điểm C và D cố định nên độ dài của các đoạn MC và MD không đổi ⇒⇒ tích MC.MD không đổi (2)
Từ (1) và (2) suy ra tích MA. MB không đổi khi cát tuyến AB thay đổi.
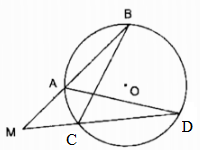
Trường hợp điểm M ở ngoài đường tròn (O)
Kẻ cát tuyến MAB bất kỳ của (O) và đường thẳng MO cắt đường tròn (O) tại C và D
Xét ∆MAD và ∆MCB:
ˆMM^ chung
ˆB=ˆDB^=D^ (hai góc nội tiếp cùng chắn cung ACAC⏜)
Suy ra: ∆MAD đồng dạng ∆MCB (g.g)
⇒MC.MA=MB.MD⇒MA.MB=MC.MD⇒MC.MA=MB.MD⇒MA.MB=MC.MD (3)
Vì M và O cố định suy ra điểm C, D cố định nên độ dài của các đoạn MC và MD không đổi ⇒⇒ tích MC. MD không đổi (4)
Từ (3) và (4) suy ra tích MA. MB không đổi khi cát tuyến MAB thay đổi.
Đúng 0
Bình luận (0)
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
mình không biết đâu chỉ có thánh mới giải được
Đúng 0
Bình luận (0)
Xét \(\Delta\)MTA và \(\Delta\)MBT
có: góc M chung
\(\widehat{MTA}=\widehat{MBT}\left(=\frac{1}{2}\widebat{AT}\right)\)
=> \(\Delta\)MTA đồng dạng \(\Delta\)MBT
=> \(\frac{MT}{MB}=\frac{MA}{MT}\Rightarrow MT^2=MA.MB\left(ĐPCM\right)\)
do MT là tiếp tuyến mà M cố định nên => MT không đổi, do vậy MA.MB không đổi
Đúng 0
Bình luận (0)
25. Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh ta luôn có MT2 = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2 cho MT = 20, MB=50cm, tính bán kính đường tròn
Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn .Qua M vẽ một cát tuyến bất kì cắt đường tròn ở A và B.Chứng minh rằng tích MA.MB không đổi
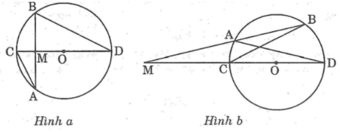
*Trường hợp M nằm bên trong đường tròn (O) (hình a)
Kẻ cát tuyến AB đi qua M và đường thẳng MO cắt đường trong tại C và D
Xét hai tam giác MBD và MCA ta có:

Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (*) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
*Trường hợp M nằm bên ngoài đường tròn (O) (hình b)
Kẻ cát tuyến MAB bất kì của (O) và đường thẳng MO cắt đường tròn tại C và D
Xét hai tam giác MCB và MAD ta có:

Ta có điểm M và O cố định ,suy ra điểm C và D cố định .Do vậy độ dài các đoạn MC và MD không đổi, suy ra tích MC.MD không đổi
Do tích MC.MD không đổi nên kết hợp với (**) suy ra tích MA.MB cũng không đổi khi cát tuyến AB thay đổi
Đúng 0
Bình luận (0)
Từ điểm M ở ngoài ( O;R ) vẽ tiếp tuyến MC và cát tuyến MAB sao cho điểm O không nằm ngoài goc BMC. MO cắt (O) tại E,F (ME<MF)Giả sử (O;R) không đổi, điểm M cố định, cát tuyến MAB quay quanh M. Hãy tìm GTLN của tống MA+MB
Cho đường tròn (O; R) cố định. Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB (A, B là các tiếp điểm). Gọi H là giao điểm của OM và AB.a) Chứng minh OM vuông góc với AB và OH.OM R2b) Từ M kẻ cát tuyến MNP với đường tròn (N nằm giữa M và P), gọi I là trung điểm của NP (I khác O). Chứng minh 4 điểm A, M, O, I cùng thuộc một đường tròn và tìm tâm của đường tròn đóc) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA và MB theo thứ tự ở C và D. Biết MA 5cm, tính chu vi tam giác...
Đọc tiếp
Cho đường tròn (O; R) cố định. Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB (A, B là các tiếp điểm). Gọi H là giao điểm của OM và AB.
a) Chứng minh OM vuông góc với AB và OH.OM = R2
b) Từ M kẻ cát tuyến MNP với đường tròn (N nằm giữa M và P), gọi I là trung điểm của NP (I khác O). Chứng minh 4 điểm A, M, O, I cùng thuộc một đường tròn và tìm tâm của đường tròn đó
c) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA và MB theo thứ tự ở C và D. Biết MA = 5cm, tính chu vi tam giác MCD.
d) Qua O kẻ đường thẳng d vuông góc với OM, cắt tia MA và MB lần lượt tại E và F. Xác định vị trí của M để diện tích tam giác MEF nhỏ nhất.
Từ điểm M ở ngoài ( O;R ) vẽ tiếp tuyến MC và cát tuyến MAB sao cho điểm O không nằm ngoài goc BMC. MO cắt (O) tại E,F (ME<MF)
Giả sử (O;R) không đổi, điểm M cố định, cát tuyến MAB quay quanh M. Hãy tìm GTLN của tống MA+MB
khó quá mk ko bít sorry!!!
547568769
Đúng 0
Bình luận (0)
Xin lỗi bạn!
Mk mới học lớp 8 thôi ak!
Chúc bạn có câu trả lời sớm nha!
Kb nhá ^_^
Đúng 0
Bình luận (0)
Khó z ak!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!?
Sorry mk ko pít cách giải =_=
Kb vs mk nhé! ^.^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho( o, r) và một điểm A cố định nằm ngoài đường tròn từ A vẽ hai tiếp tuyến AB AC (A, C là hai tiếp điểm vẽ cát tuyến AMN thay đổi của O (M nằm giữa A, N) . Từ M kẻ tiếp tuyến Với O cắt AB AC thứ tự tại P, Q. Tìm vị trí cát tuyến AMN để BP+CQ đạt giá trị nhỏ nhất
















