TÌM BỐN SỐ NGUYÊN BIẾT TỔNG BA TRONG BỐN SỐ LẦN LƯỢT LÀ 11;-21;34;0
!!!!! AI LÀM NHANH VÀ ĐÚNG MÌNH TICK CHO !!!!!
Những câu hỏi liên quan
Câu hỏi : Tìm 4 số nguyên biết tổng ba trong bốn số lần lượt là 11 ; -21 ; 34 ; 0
GIÚP MÌNH VỚI , AI NHANH MÌNH K
Cho bốn số tự nhiên. Biết tổng các số là 43 . Nếu lấy số thứ nhất trừ đi 2, số thứ hai nhân 3 , số thứ ba cộng 6 và bốn lần số thứ tư cộng 3 thì ta được số bằng nhau.
Vậy bốn số cần tìm lần lượt là
Cho bốn số nguyên dương, trong đó ba số đầu lập thành một cấp số cộng, ba số sau lập thành cấp số nhân. Biết tổng số hạng đầu và cuối là 37, tổng hai số hạng giữa là 36, tìm bốn số đó. A. b 15 ; c 20 ; d 25 ; a 12 B. b 16 ; c 20 ; a 12 ; d 25 C. b 15 ; c 25 ; d 25 ; a 12 D. b 16 ; c 20 ; d 25 ; a 18
Đọc tiếp
Cho bốn số nguyên dương, trong đó ba số đầu lập thành một cấp số cộng, ba số sau lập thành cấp số nhân. Biết tổng số hạng đầu và cuối là 37, tổng hai số hạng giữa là 36, tìm bốn số đó.
A. b = 15 ; c = 20 ; d = 25 ; a = 12
B. b =16 ; c = 20 ; a = 12 ; d = 25
C. b = 15 ; c = 25 ; d = 25 ; a = 12
D. b =16 ; c = 20 ; d = 25 ; a = 18
Chọn B.
Gọi bốn số đó là a ;b ;c ;d ta có hệ:
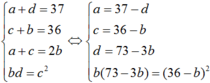
Giải ra ta được : b = 16 ; c = 20 ; d = 25 ; a = 12.
Đúng 0
Bình luận (0)
16 tháng 8 2021 lúc 14:37
1. Ta biết rằng có 25 số nguyên tố nhỏ hơn 100. Tổng của 25 số nguyên tố đó là chẵn hay lẻ?
2. Tổng của ba số nguyên tố bằng 1012. Tìm số nhỏ nhất trong ba số nguyên tố đó.
3. Tìm bốn số nguyên tố liên tiếp, sao cho tổng của chúng là số nguyên tố.
1. Ta có: trong 25 số nguyên tố có 1 số nguyên tố chẵn còn lại là 24 số nguyên tố lẻ. Tổng của 24 số lẻ là một số chẵn nên tổng của 25 số nguyên tố nhỏ hơn 100 là số chẵn.
Đúng 3
Bình luận (0)
Ta có: Gỉa sử 3 số nguyên tố đó đều là lẻ thì lẻ+lẻ+lẻ=lẻ
⇒Có một số nguyên tố chẵn
Chỉ 2 là số nguyên tố chẵn duy nhất
⇒Số nhỏ nhất trong ba số nguyên tố là 2
Đúng 1
Bình luận (1)
Trung bình cộng của ba số là 288. Tìm số thứ ba, biết số thứ nhất gấp bốn lần số thứ hai, số thứ hai gấp ba lần số thứ ba.
Trả lời: Ba số viết theo thứ tự lần lượt là: ; ; .
Số thứ nhất: 648
Số thứ hai: 162
Số thứ ba: 54
Đúng 2
Bình luận (0)
Cho bốn số nguyên dương, trong đó ba số đầu lập thành một cấp số cộng, ba số sau lập thành cấp số nhân. Biết tổng số hạng đầu và cuối là 37, tổng hai số hạng giữa là 36, tìm hai số đầu tiên. A. 16 và 20 B.20 và 25 C.12 và 18 D. 12 và 16
Đọc tiếp
Cho bốn số nguyên dương, trong đó ba số đầu lập thành một cấp số cộng, ba số sau lập thành cấp số nhân. Biết tổng số hạng đầu và cuối là 37, tổng hai số hạng giữa là 36, tìm hai số đầu tiên.
A. 16 và 20
B.20 và 25
C.12 và 18
D. 12 và 16
Tìm bốn số, biết tổng bốn số bằng 238 và số thứ nhất gấp 2 lần số thứ hai, số thứ hai gấp 3 lần số thứ ba, số thứ ba bằng ¼ số thứ tư.
8 tháng 10 2023 lúc 20:12
Trong một câu hỏi của Đường Lên Đỉnh Olympia lần thứ 23 có một câu hỏi như sau:
Cho bốn số nguyên dương phân biệt sao cho tổng của mỗi hai số chia hết cho 2 và tổng của mỗi ba số chia hết cho 3. Tìm giá trị nhỏ nhất của tổng bốn số này?
Bằng cách giải đơn giản, các bạn hãy giải thật nhanh bài toán đưa ra.
Đọc tiếp
Trong một câu hỏi của Đường Lên Đỉnh Olympia lần thứ 23 có một câu hỏi như sau:
"Cho bốn số nguyên dương phân biệt sao cho tổng của mỗi hai số chia hết cho 2 và tổng của mỗi ba số chia hết cho 3. Tìm giá trị nhỏ nhất của tổng bốn số này?"
Bằng cách giải đơn giản, các bạn hãy giải thật nhanh bài toán đưa ra.
Từ dữ kiện thứ hai, ta thấy 4 số có cùng số dư khi chia cho 3 nên tổng nhỏ nhất là \(1+7+13+19=40\) (giữ lại đáp án ban đầu nhé)
Đúng 2
Bình luận (0)
Từ dữ kiện thứ nhất ta thấy hoặc cả 4 số đều lẻ, hoặc cả 4 số đều chẵn.
Từ dữ kiện thứ 2 ta thấy cả 4 số đều phải chia hết cho 3.
Suy ra tổng nhỏ nhất của 4 số là \(1+7+13+19=40\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho bốn số nguyên biết rằng ba số hạng đầu lập thành mọt cấp số nhân, ba số hạng sau lập thành một cấp số cộng. Tổng của hai số hạng đầu và cuối bằng 14, còn tổng hai số ở giữa bằng 12. Tổng của bốn số nguyên đó là?
A. 20
B. 22
C. 24
D. 26
Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
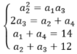
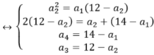
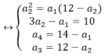
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D
Đúng 0
Bình luận (0)