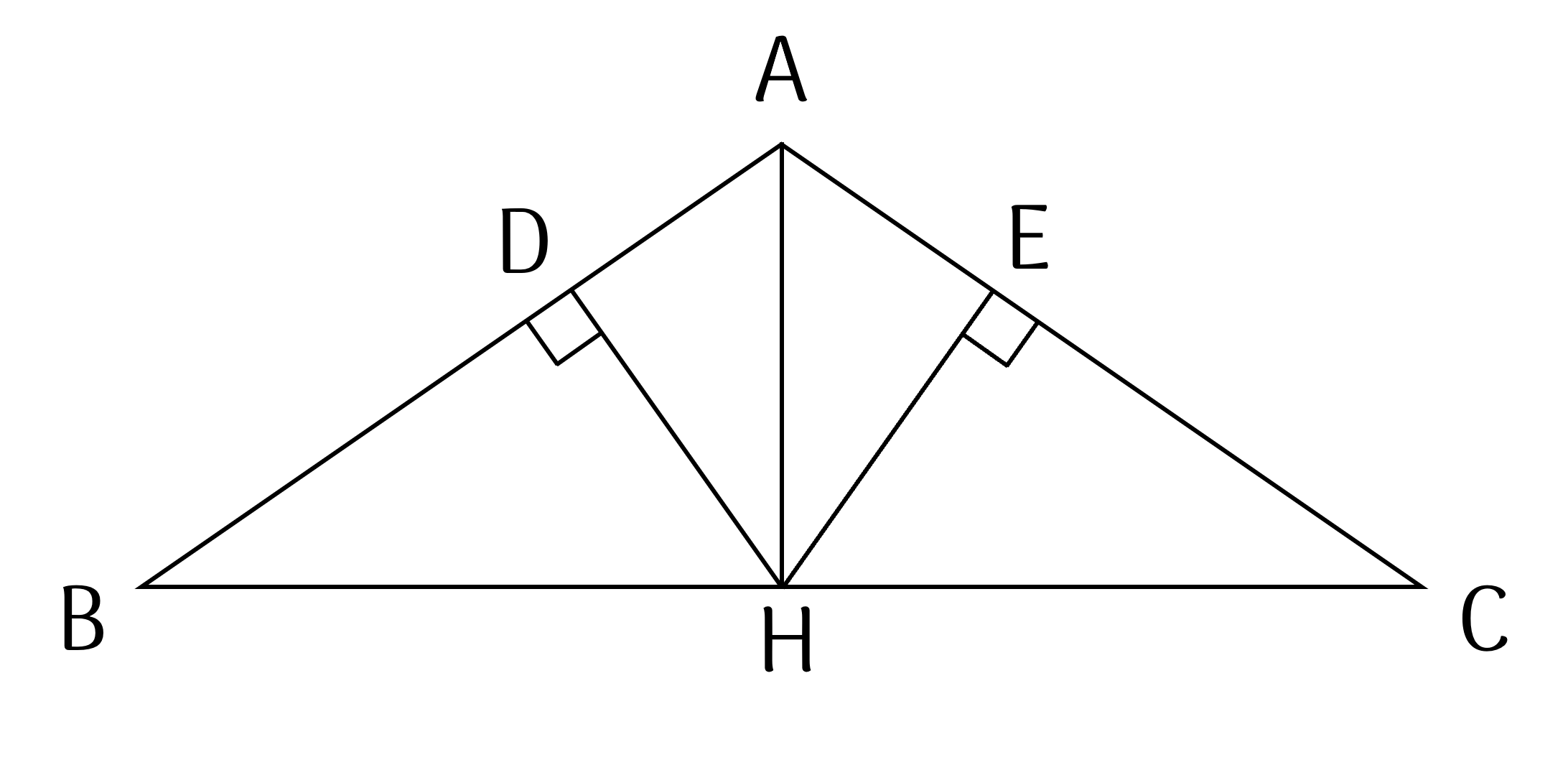
cho tam giác cân AMN có góc MAN =\(^{120^0}\). Vẽ đường cao AH ( H thuộc MN )
a, Chứng minh AH là tia phân giác của góc MAN
b, Kẻ HD vuông góc với AM ( D thuộc AM ) , kẻ HE vuông góc với AN ( E thuộc AN ). Chứng minh tam giác ADE cân và DE song song với MN
c,Chứng minh tam giác HDE đều
d, Đường vuông góc với MN kẻ từ N cắt MA tại I. Tính độ dài cạnh AI biết NI = 10cm