Tìm m lớn nhất để hàm số \(\dfrac{1}{3}\)x3 – mx2 + (4m-3)x+2017 đồng biến trên R

Những câu hỏi liên quan
Cho hàm số
y
1
3
x
3
-
m
x
2
+
(
4
m
-
3
)
x
+
2017
. Tìm gi...
Đọc tiếp
Cho hàm số y = 1 3 x 3 - m x 2 + ( 4 m - 3 ) x + 2017 . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên R
A.m=2
B.m=3
C.m=4
D.m=1
Tìm m lớn nhất để hàm số
y
1
3
x
3
−
m
x
2
+
4
m
−
3
x
+
2017
đồng biến trên R ? A. m1 B. m2 C. m0 D. m3
Đọc tiếp
Tìm m lớn nhất để hàm số y = 1 3 x 3 − m x 2 + 4 m − 3 x + 2017 đồng biến trên R ?
A. m=1
B. m=2
C. m=0
D. m=3
Đáp án D
Ta có: y ' = x 2 − 2 m x + 4 m − 3 . Để hàm số đồng biến trên R thì y ' ≥ 0 ∀ x ∈ ℝ
⇔ Δ ' = m 2 − 4 m + 3 ≤ 0 ⇔ 1 ≤ m ≤ 3 ⇒ m lớn nhất bằng 3
Đúng 0
Bình luận (0)
Cho hàm số y
1
3
x
3
-
m
x
2
+
(
4
m
-
3
)
x
+
2017
. Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên . A. m 2 B. m 3 C. m 4 D. m 1
Đọc tiếp
Cho hàm số y = 1 3 x 3 - m x 2 + ( 4 m - 3 ) x + 2017 . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên .
A. m = 2
B. m = 3
C. m = 4
D. m = 1
Chọn B
Phương pháp:
Tính y', để hàm số đồng biến trên
ℝ
thì ![]() (y' = 0 tại hữu hạn điểm)
(y' = 0 tại hữu hạn điểm)
Sử dụng ![]()
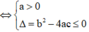
Cách giải:
Tập xác định D = ℝ
Đạo hàm ![]()
Để hàm số đồng biến trên
ℝ
thì ![]() (y' = 0 tại hữu hạn điểm)
(y' = 0 tại hữu hạn điểm)
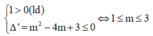
Suy ra giá trị lớn nhất của tham số m thỏa mãn ycbt là m = 3
Đúng 0
Bình luận (0)
Trong tất cả các giá trị của tham số mm để hàm số y=\dfrac{1}{3} x^{3} +mx^{2} -mx-my=31x3+mx2−mx−m đồng biến trên \mathbb{R},R, giá trị nhỏ nhất của mm là
Tìm m để hàm số
y
x
3
+
m
x
2
+
1
−
2
m
x
+
m
−
3
đồng biến trên khoảng (-3;0) A.
m
≥
2
3
+
3
B.
m
≤
2
3
−...
Đọc tiếp
Tìm m để hàm số y = x 3 + m x 2 + 1 − 2 m x + m − 3 đồng biến trên khoảng (-3;0)
A. m ≥ 2 3 + 3
B. m ≤ 2 3 − 3
C. m ≤ 6 + 42
D. m ≥ 6 − 42
Đáp án B
Ta có y ' = 3 x 2 + 2 m x + 1 − 2 m
Hàm số đồng biến trên − 3 ; 0 ⇔ y ' ≥ 0 , ∀ x ∈ − 3 ; 0 ⇔ 3 x 2 + 2 m x + 1 − 2 m ≥ 0 , ∀ x ∈ − 3 ; 0
⇔ m 2 x − 2 ≥ − 3 x 2 − 1 ⇔ m ≤ − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 1
Xét hàm số
f x = − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 ⇒ f ' x = − 6 x 2 + 12 x + 2 2 x − 2 2 ⇒ f ' x = 0 ⇔ x = 3 ± 2 3 3
Ta có bảng biến thiên hàm số f x như sau:
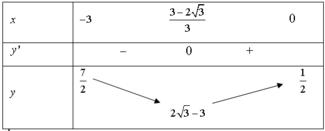
Suy ra f x − 3 ; 0 ≥ 2 3 − 3 ⇒ 1 ⇔ m ≤ 2 3 − 3
Đúng 0
Bình luận (0)
Tìm các giá trị thực của m để mỗi tiếp tuyến của đồ thị hàm số
y
x
3
−
mx
2
−
2
mx
+
2017
đều là đồ thị của hàm số bậc nhất đồng biến. A.
m
6
m...
Đọc tiếp
Tìm các giá trị thực của m để mỗi tiếp tuyến của đồ thị hàm số y = x 3 − mx 2 − 2 mx + 2017 đều là đồ thị của hàm số bậc nhất đồng biến.
A. m > 6 m < 0
B. 0 < m < 6
C. − 6 < m < 0
D. m < − 6 m > 0
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
+
m
x
2
−
m
x
đồng biến trên R. A.
−
3
≤
m
≤
0
B.
−
3
m
0
C.
m
≤
−...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + m x 2 − m x đồng biến trên R.
A. − 3 ≤ m ≤ 0
B. − 3 < m < 0
C. m ≤ − 3 m ≥ 0
D. m < − 3 m > 0
Đáp án A
Ta có: y ' = 3 x 2 + 2 m x − m .
Hàm số đồng biến trên ℝ ⇔ y ' ≥ 0 , ∀ x ∈ ℝ
⇒ Δ ' y ' ≤ 0 ⇔ m 2 + 3 m ≤ 0 ⇔ − 3 ≤ m ≤ 0.
Đúng 0
Bình luận (0)
Tìm tất cả giá trị của tham số m để hàm số
y
1
3
(
m
2
−
2
m
)
x
3
+
m
x
2
+
3
x
đồng biến trên R A.
m
0.
B.
1
m
≤
3.
C.
m...
Đọc tiếp
Tìm tất cả giá trị của tham số m để hàm số y = 1 3 ( m 2 − 2 m ) x 3 + m x 2 + 3 x đồng biến trên R
A. m < 0.
B. 1 < m ≤ 3.
C. m < 0 m ≥ 3 .
D. m ≤ 0 m ≥ 3 .
Tìm tập hợp tất cả các tham số m để hàm số
y
x
3
–
m
x
2
+
(
m
–
1
)
x
+
1
đồng biến trên khoảng (1; 2) A.
m
≤
11
3
B. m
11
3
C.
m
≤
2
D. m 2
Đọc tiếp
Tìm tập hợp tất cả các tham số m để hàm số y = x 3 – m x 2 + ( m – 1 ) x + 1 đồng biến trên khoảng (1; 2)
A. m ≤ 11 3
B. m < 11 3
C. m ≤ 2
D. m < 2











