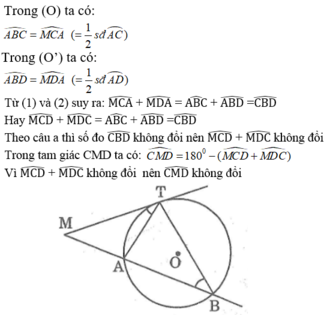
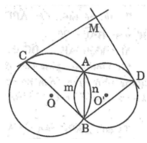
Cho 2 đường tròn o và o' cắt nhău tại A và B .Qua A kẻ đường tròn cát tuyến cắt đường tròn o tại C,cắt đường tròn O' tại D.Chứng minh ACD có số đo các góc không đổi,từ đó xác định vị trí của cát tuyến CD có độ dài lớn nhất

Những câu hỏi liên quan
Cho 2 đường tròn (O) và (O') cắt nhau tại A và B(O và O' nằm khác phía vs AB).Qua A kẻ cát tuyến cắt đường tròn (O) ở C.Cắt (O') ở D.Các tiếp tuyến của 2 đường tròn kẻ từ C và D,cắt nhau ở I.Chứng minh rằng khi cát tuyến CAD thay đổi thì:
a)Góc CBD ko đổi
b)Góc CID ko đổi
Cho hai đường tròn (O) và (O') cắt nhau tại A và B sao cho O và O' nằm khác phía với AB. Qua A kẻ cát tuyến cắt (O) và (O') lần lượt tại M và N. Tiếp tuyến của (O) tại M cắt tiếp tuyến của (O') tại N ở C. Xác định vị trí của cát tuyến MAN để bán kính đường tròn ngoại tiếp tam giác MCN đạt giá trị lớn nhất
*Bài 1: Hai đường tròn (O) và (O) cắt nhau tại A và B. Đường thẳng qua A cắt đường tròn (O) tại điểm C và cắt đường tròn (O) tại điểm Da) Chứng minh khi đường thẳng quay quanh A thì widehat{CBD}có sđ không đổib) Từ C và D vẽ 2 tiếp tuyến với đường tròn. CMR góc tạo bởi 2 tiếp tuyến này có số đo không đổi khi cát tuyến CAD quay quanh A*Bài 2: Từ điểm M ở ngoài đường tròn (O), kẻ tiếp tuyến MT (T là tiếp điểm) và cát tuyến MAB qua O ( A,Binđường tròn, A ở giữa M và D). CM: widehat{AMT}+widehat{MT...
Đọc tiếp
*Bài 1: Hai đường tròn (O) và (O') cắt nhau tại A và B. Đường thẳng qua A cắt đường tròn (O) tại điểm C và cắt đường tròn (O') tại điểm D
a) Chứng minh khi đường thẳng quay quanh A thì \(\widehat{CBD}\)có sđ không đổi
b) Từ C và D vẽ 2 tiếp tuyến với đường tròn. CMR góc tạo bởi 2 tiếp tuyến này có số đo không đổi khi cát tuyến CAD quay quanh A
*Bài 2: Từ điểm M ở ngoài đường tròn (O), kẻ tiếp tuyến MT (T là tiếp điểm) và cát tuyến MAB qua O ( A,B\(\in\)đường tròn, A ở giữa M và D). CM: \(\widehat{AMT}+\widehat{MTA}=90^o\)
Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C ∈ (O) ,D ∈ (O’)). Từ C và D vẽ hai tiếp tuyến với đường tròn.Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Qua A kẻ cát tuyến cắt đường tròn (O) tại C, cắt đường tròn (O') tại D sao cho CD vuông góc với AB, đường thẳng CB cắt đường tròn (O) tại M, đường thẳng DB cắt đường tròn (O') tại N. Chứng minh AB là tia phân giác của góc MAN
Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C ∈ (O) ,D ∈ (O’)). Chứng minh rằng khi cát tuyến quay xung quanh điểm A thì ∠ CBD có số đo không đổi
cho đường tròn tâm o cắt đường tròn tâm O' tại A và B. Từ đường thẳng AB lấy điểm M kẻ TM là tiếp tuyến của đường tròn tâm O và từ M kẻ cát tuyến cắt đường tròn tâm O' tại C và D. Chứng minh: MT^2=MC.MD
Cho đường tròn tâm O, đường kính AB . M cố định trên tiếp tuyến tại A của đường tròn (O) vẽ tiếp tuyến MC và cát tuyến MHK ( Nằm giữa 2 tia MB và MO ) .Đường thẳng BH , BK cắt đường thẳng MO tại E,F . Qua A kẻ đt // với MK cắt đường tròn tại I . CI cắt MK tại N a, Tứ giác MCHE nội tiếp b, Chứng minh tổng MN2 + ON2 không phụ thuộc vào vị trí của cát tuyến MHK c, Chứng minh OE OF
Đọc tiếp
Cho đường tròn tâm O, đường kính AB . M cố định trên tiếp tuyến tại A của đường tròn (O) vẽ tiếp tuyến MC và cát tuyến MHK ( Nằm giữa 2 tia MB và MO ) .Đường thẳng BH , BK cắt đường thẳng MO tại E,F . Qua A kẻ đt // với MK cắt đường tròn tại I . CI cắt MK tại N
a, Tứ giác MCHE nội tiếp
b, Chứng minh tổng MN2 + ON2 không phụ thuộc vào vị trí của cát tuyến MHK
c, Chứng minh OE = OF
Từ điểm A nằm ngoài đường tròn (O), vẽ cát tuyến ABC với đường tròn. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K. Qua K kẻ đường thẳng vuông góc với AO, cắt AO tại H và đường tròn (O) tại E và F (E nằm giữa K và F). Gọi M là giao điểm của OK và BC.gọi D là giao điểm của BC và EF chứng minh DB.AC =DC.AB