Các câu hỏi tương tự
Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C ∈ (O) ,D ∈ (O’)). Từ C và D vẽ hai tiếp tuyến với đường tròn.Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A
*Bài 1: Hai đường tròn (O) và (O) cắt nhau tại A và B. Đường thẳng qua A cắt đường tròn (O) tại điểm C và cắt đường tròn (O) tại điểm Da) Chứng minh khi đường thẳng quay quanh A thì widehat{CBD}có sđ không đổib) Từ C và D vẽ 2 tiếp tuyến với đường tròn. CMR góc tạo bởi 2 tiếp tuyến này có số đo không đổi khi cát tuyến CAD quay quanh A*Bài 2: Từ điểm M ở ngoài đường tròn (O), kẻ tiếp tuyến MT (T là tiếp điểm) và cát tuyến MAB qua O ( A,Binđường tròn, A ở giữa M và D). CM: widehat{AMT}+widehat{MT...
Đọc tiếp
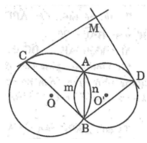
*Bài 1: Hai đường tròn (O) và (O') cắt nhau tại A và B. Đường thẳng qua A cắt đường tròn (O) tại điểm C và cắt đường tròn (O') tại điểm D
a) Chứng minh khi đường thẳng quay quanh A thì \(\widehat{CBD}\)có sđ không đổi
b) Từ C và D vẽ 2 tiếp tuyến với đường tròn. CMR góc tạo bởi 2 tiếp tuyến này có số đo không đổi khi cát tuyến CAD quay quanh A
*Bài 2: Từ điểm M ở ngoài đường tròn (O), kẻ tiếp tuyến MT (T là tiếp điểm) và cát tuyến MAB qua O ( A,B\(\in\)đường tròn, A ở giữa M và D). CM: \(\widehat{AMT}+\widehat{MTA}=90^o\)
Cho (O) và (O') cắt nhay tại A và B. Qua A kẻ cát tuyến CAD (C thuộc (O) và D thuộc (O'))
CM khi cát tuyến CAD quay quanh A thì \(\widehat{CBD}\)có số đo không đổi
Từ điểm M nằm bên ngoài đường tròn (O), vẽ tiếp tuyến MA và cát tuyến MCB với A,B,C Î (O). Phân giác góc
B
A
C
^
cắt BC tại D, cắt (O) tại N. Chứng minh:a, MA MDb, Cho cát tuyến MCB quay quanh M và luôn cắt đưòng tròn. Chứng minh MB.MC không đổic,
N
B
2
N...
Đọc tiếp
Từ điểm M nằm bên ngoài đường tròn (O), vẽ tiếp tuyến MA và cát tuyến MCB với A,B,C Î (O). Phân giác góc B A C ^ cắt BC tại D, cắt (O) tại N. Chứng minh:
a, MA = MD
b, Cho cát tuyến MCB quay quanh M và luôn cắt đưòng tròn. Chứng minh MB.MC không đổi
c, N B 2 = N A . N D
Cho đường tròn (O) và đường thẳng xy không có điểm chung với đường tron f(O). Gọi A là hình chiếu của O trên đường thẳng xy. Qua A vẽ cát tuyến không đi qua O cắt đường tròn tại hai điểm B và C (AB AC). Tiếp tuyến của đường tròn tại hai điểm B và C cắt đường thẳng xy lần lượt taiij M và N.a) Chứng minh tứ giác ABOM nội tiếp.b) Chứng minh góc BCO bằng góc ANO và tam giác OMN cân.c) Giả sử đường tròn (O) và đường thẳng xy cố định. Từ M vẽ tiếp tuyến thứ hai ME với đường tròn (O), E là tiếp điểm k...
Đọc tiếp
Cho đường tròn (O) và đường thẳng xy không có điểm chung với đường tron f(O). Gọi A là hình chiếu của O trên đường thẳng xy. Qua A vẽ cát tuyến không đi qua O cắt đường tròn tại hai điểm B và C (AB < AC). Tiếp tuyến của đường tròn tại hai điểm B và C cắt đường thẳng xy lần lượt taiij M và N.
a) Chứng minh tứ giác ABOM nội tiếp.
b) Chứng minh góc BCO bằng góc ANO và tam giác OMN cân.
c) Giả sử đường tròn (O) và đường thẳng xy cố định. Từ M vẽ tiếp tuyến thứ hai ME với đường tròn (O), E là tiếp điểm khác B. Chứng minh khi cát tuyến ABC di chuyển quanh A thì BE luôn đi qua một điểm cố định.
GIÚP MÌNH CÂU C VỚI!!!
Cho (O) và (O') cắt nhau tại A và B, kẻ đường kính AC của (O) và đường kính AD của (O'). Vẽ cát tuyến của 2 đường tròn, cát tuyến này cắt (O) tại P và (O') tại Q. PM song song với CD
a) Chứng minh 3 điểm C, B, D thẳng hàng
b) Chứng minh CPMD là hình bình hành
c) Tìm quỹ tích điểm M khi cát tuyến PQ quay quanh điểm A
Cho (O) và (O') cắt nhau tại A và B, kẻ đường kính AC của (O) và đường kính AD của (O'). Vẽ cát tuyến của 2 đường tròn, cát tuyến này cắt (O) tại P và (O') tại Q. PM song song với CD
a) Chứng minh 3 điểm C, B, D thẳng hàng
b) Chứng minh CPMD là hình bình hành
c) Tìm quỹ tích điểm M khi cát tuyến PQ quay quanh điểm A
Cho (O) và (O) cắt nhau tại A; B. Vé đường kính AC của (O), đường kính AD của (O). a) Chứng minh: C, B, D thẳng hàng b) Qua A vẽ cát tuyến bất kỳ cắt (O) và (O) tại E, F. Tứ giác CEFD là hình gì? Vì sao? c) Chứng minh:widehat{EBF}không đổi khi cát tuyến EAF quay quanh A. d) Từ E, F vẽ xhai cát tuyến với (O) và (o). Chứng minh: hai tiếp tuyến cùng hợp với nhau một góc không đổi
Đọc tiếp
Cho (O) và (O') cắt nhau tại A; B. Vé đường kính AC của (O), đường kính AD của (O').
a) Chứng minh: C, B, D thẳng hàng
b) Qua A vẽ cát tuyến bất kỳ cắt (O) và (O') tại E, F. Tứ giác CEFD là hình gì? Vì sao?
c) Chứng minh:\(\widehat{EBF}\)không đổi khi cát tuyến EAF quay quanh A.
d) Từ E, F vẽ xhai cát tuyến với (O) và (o'). Chứng minh: hai tiếp tuyến cùng hợp với nhau một góc không đổi
Từ một điểm M nằm ngoài đường tròn (O) kẻ các tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm). Một cát tuyến qua M, cắt (O) tại hai điểm C và D ( C nằm giữa M và D).
a) Chứng minh: AC.DB=AD.CB
b) Phân giác CAD cắt CD tại I. Chứng minh BI là phân giác góc CBD.