cho tam giác đều ABC, tìm các phép quay có đỉnh là đỉnh tam giác, góc 60 độ

Những câu hỏi liên quan
cho tam giác ABC có tâm O (các đỉnh ghi theo chiều kim đồng hồ )
a,tìm ảnh của B ,đoạn thẳng BC qua phép quay tâm O góc quay 60 độ
b,tìm ảnh của tam giác OAB qua phép quay tâm O góc quay -120 độ
c, tìm ảnh của tam giác ABC qua phép quay tâm A góc quay tam giác
cho Δ đều ABC, tìm các phép quay có đỉnh là đỉnh Δ, góc 60 độ
Trong mặt phẳng Oxy cho các điểm A(-3;2), B(-4;5) và C(-1;3).a. Chứng minh rằng các điểm A’(2;3), B’(5;4) và C’(3;1) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc
–
90
o
.b. Gọi tam giác
A
1
B
1
C
1
là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc
–...
Đọc tiếp
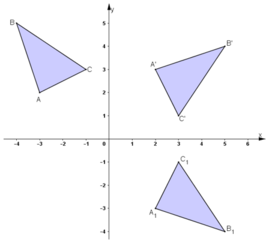
Trong mặt phẳng Oxy cho các điểm A(-3;2), B(-4;5) và C(-1;3).
a. Chứng minh rằng các điểm A’(2;3), B’(5;4) và C’(3;1) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc – 90 o .
b. Gọi tam giác A 1 B 1 C 1 là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc – 90 o và phép đối xứng qua trục Ox. Tìm tọa độ các đỉnh của tam giác A 1 B 1 C 1 .
+ Chứng minh hoàn toàn tương tự ta được
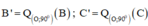
b. ΔA1B1C1 là ảnh của ΔABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc –90º và phép đối xứng qua trục Ox.
⇒ ΔA1B1C1 là ảnh của ΔA’B’C’ qua phép đối xứng trục Ox.
⇒ A1 = ĐOx(A’) ⇒ A1(2; -3)
B1 = ĐOx(B’) ⇒ B1(5; -4)
C1 = ĐOx(C’) ⇒ C1(3; -1).
a) + Ta có:
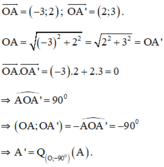
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc ngoài đỉnh C bằng 120 độ ,A -B =60 độ .Tính các góc của tam giác ABC
Iu mn nhìu !
Vì góc ngoài đỉnh C bằng 120 độ nên \(\widehat{A}+\widehat{B}=120^0\)
Mà \(\widehat{A}-\widehat{B}=60^0\Rightarrow\left\{{}\begin{matrix}\widehat{A}=\left(120^0+60^0\right):2=90^0\\\widehat{B}=120^0-90^0=30^0\end{matrix}\right.\)
\(\Rightarrow\widehat{C}=180^0-90^0-30^0=60^0\)
Đúng 1
Bình luận (1)
Cho tam giác ABC có ba góc đều khác 120 độ. Tìm trong tam giác điểm M sao cho tổng các khoảng cách từ M đến 3 đỉnh của tam giác là nhỏ nhất.
Cho đa giác đều 91 đỉnh. Mỗi đỉnh được tô bởi màu đỏ hoặc màu xanh, CMR: luôn tìm được 3 đỉnh trong 91 đỉnh của đa giác thoả:
-3 đỉnh cùng màu và là 3 đỉnh của 1 tam giác cân có ít nhất 1 góc nhỏ hơn 60 độ.
Cho tam giác ABC có Góc A = 40 độ; góc B= 60 độ. góc ACD là góc ngoài tại đỉnh C của tam giác ABC. Tính góc C và góc ACD?
Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 2a, góc giữa cạnh bên và mặt đáy bằng 60 độ. Tính thể tích của khối nón có đỉnh là S và đáy là đường ngoại tiếp tam giác ABC
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\)
\(\Rightarrow\widehat{SAO}=60^0\Rightarrow AO=SA.cos60^0=a\)
\(R=a;l=2a\Rightarrow h=SO=\sqrt{\left(2a\right)^2-a^2}=a\sqrt{3}\)
\(V=\dfrac{1}{3}\pi R^2h=\dfrac{\sqrt{3}}{3}\pi a^3\)
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC có trực tâm H và góc BAC =60 độ. Gọi M,N,P lần lượt là chân đường cao hạ từ các đỉnh A,B,C của tam giác ABC và I là trung điểm của BC.
a) chứng minh tam giác NIP đều
b) Giả sử IA là phân giác của góc NIP. Tính số đo của góc BCP
e làm chứng minh dc góc NPI = BAC=60 độ, thế e ghi tương tự vs góc PNI=BAC=60 độ dc k ạ
Đúng 0
Bình luận (0)














