cho tam giác ABC vuông tại A ,D là điểm tuyf ý trên cạnh BC (D khác B ;D khác C ) gọi E và F là hình chiếu của D lên trên cạch AB và AC .CMR :
a) tứ giác AEDF là hình gì chứng minh
b)tam giác ABC có thêm gì để EDFA là hình vuông
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, D là điểm tùy ý thuộc cạnh BC ( D khác B, D khác C), Gọi E và F lần lượt là hình chiếu vuông góc của D trên cạnh AB và AC
a) Tứ giác AEDF là hình gì ? vì sao ?
b) Xác định vị trí của D trên cạnh BC để EF có độ dài ngắn nhất?
c) Tam giác vuông ABC có thêm điều kiện gì thì tứ giác EDF là hình vuông ?
cho tam giác ABC vuông cân tại đỉnh A, M là trung điểm của BC. trên cạnh BC, lấy điểm D tùy ý (D khác M). từ B, C hạ BE, CF vuông góc AD. CM:
a) tam giác AEB= tam giác AFC
b) tam giác AME= tam giác CMF
c) tam giác MEF vuông cân
cho tam giác ABC vuông cân đỉnh A, M là trung điểm của BC. Trên cạnh BC lấy điểm D tùy ý ( D khác M). Từ B,C hạ BE, CF vuông góc với AD. Chứng minh: a;tam giác AEB=AFC b; tam giác AME=CME c;tam giác MEF vuông cân
Cho tam giác ABC vuông tại đỉnh A, M là trung điểm BC.Trên cạnh BC, lấy điểm D tùy ý ( D khác M). Từ B,C hạ BE, CF vuông góc AD . CM:
a, tam giác AEB = tam giác AFC
b, tam giác AME = tam giác CMF
c, tam giác MEF vuông cân
giúp mình vs
Cho tam giác ABC vuông tại A, D là điểm tùy ý thuộc cạnh BC (D B, D C). Gọi E và F lần
lượt là hình chiếu vuông góc của D trên cạnh AB và AC.
a) Tứ giác AEDF là hình gì ? Vì sao ?
b) Xác định vị trí của D trên cạnh BC để EF có độ dài ngắn nhất ?
1,Cho tam giác ABC. Trên cạnh AC lấy điểm E cố định , trên cạnh BC lấy điểm F cố định ( E khác A và C; F khác B và C). Trên cạnh AB lấy điểm D di động ( D khác A và B) . Hãy xác định vị trí điểm D trên đường thẳng AB sao cho DE^2+DF^2 có giá trị nhỏ nhất. 2,Cho tam giác ABC vuông tại A có đường cao AH. Gọi I là tâm đg tròn nội tiếp tam giác, E,F,D lần lượt là hình chiếu của I trên AC, AB,BC.Gọi M là trung điểm AC.MI cắt AB tại N.FD cắt AH tại P. Chứng minh ANAP
Đọc tiếp
1,Cho tam giác ABC. Trên cạnh AC lấy điểm E cố định , trên cạnh BC lấy điểm F cố định ( E khác A và C; F khác B và C). Trên cạnh AB lấy điểm D di động ( D khác A và B) . Hãy xác định vị trí điểm D trên đường thẳng AB sao cho DE^2+DF^2 có giá trị nhỏ nhất.
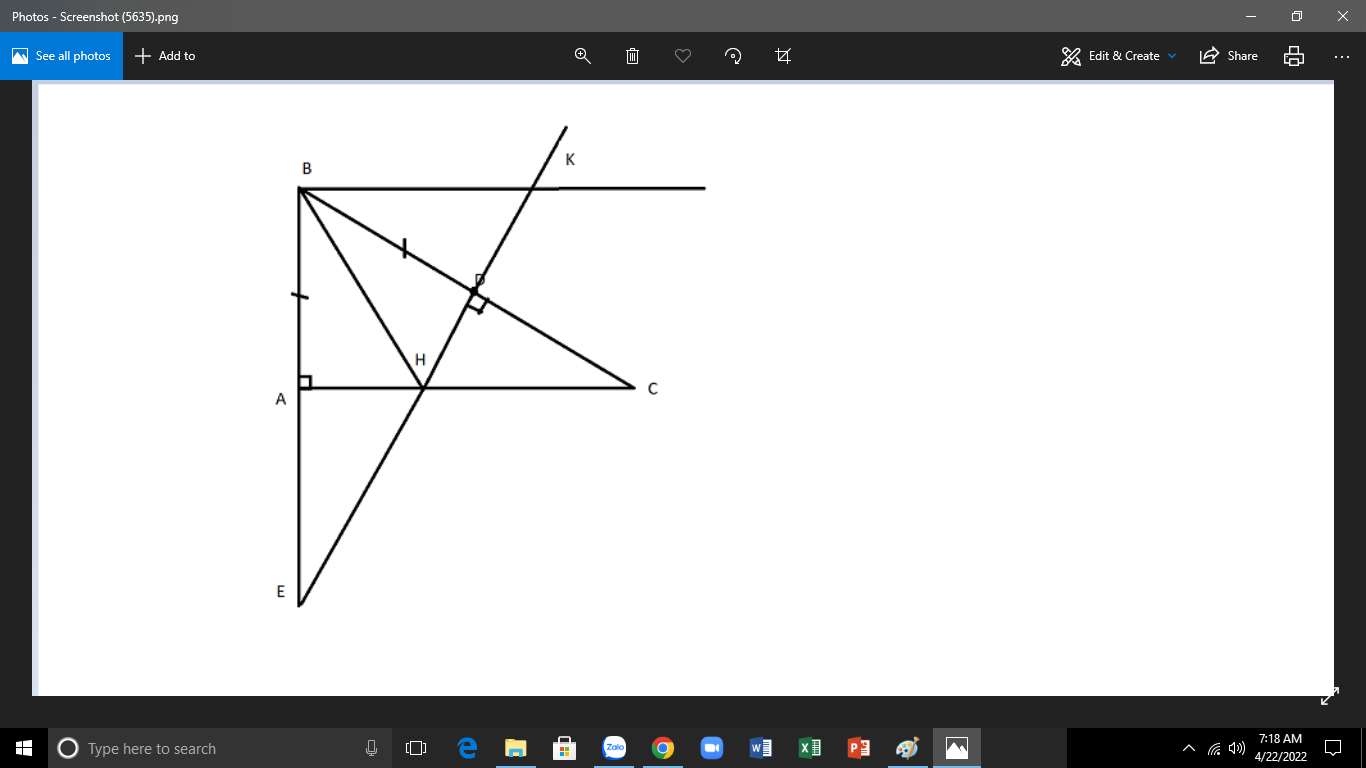
2,Cho tam giác ABC vuông tại A có đường cao AH. Gọi I là tâm đg tròn nội tiếp tam giác, E,F,D lần lượt là hình chiếu của I trên AC, AB,BC.Gọi M là trung điểm AC.MI cắt AB tại N.FD cắt AH tại P. Chứng minh AN=AP
Lưu ý: Phải vẽ hìnhCho tam giác ABC vuông tại A và ABC 60 độa, So sánh AB và ACb, Trên cạnh BC lấy điểm D sao cho BD AB. Qua D dựng đường thẳng vuông góc với BC cắt tia đối Ab tại E. Chứng minh : ABC tam giác DBEc, Gọi H là giao điểm của ED và AC . Chứng minh: tia BH là tia phân giác của góc ABC?d, Qua B dựng dường vuông góc với AB ,cắt ED tại K. Chứng minh : Δ HBK đều
Đọc tiếp
Lưu ý: Phải vẽ hình
Cho tam giác ABC vuông tại A và ABC = 60 độ
a, So sánh AB và AC
b, Trên cạnh BC lấy điểm D sao cho BD = AB. Qua D dựng đường thẳng vuông góc với BC cắt tia đối Ab tại E. Chứng minh : ABC = tam giác DBE
c, Gọi H là giao điểm của ED và AC . Chứng minh: tia BH là tia phân giác của góc ABC?
d, Qua B dựng dường vuông góc với AB ,cắt ED tại K. Chứng minh : Δ HBK đều
\(\text{a)Xét }\Delta ABC\text{ có:}\)
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(\text{tính chất tổng ba góc một tam giác}\right)\)
\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)\)
\(\Rightarrow\widehat{C}=180^0-\left(90^0+60^0\right)=30^0\)
\(\text{Xét }\Delta ABC\text{ có:}\)
\(\widehat{A}>\widehat{B}>\widehat{C}\left(90^0>60^0>30^0\right)\)
\(\Rightarrow BC>AC>AB\left(\text{quan hệ giữa góc và cạnh đối diện trong tam giác}\right)\)
\(\Rightarrow AB< AC\)
\(b)\text{Xét }\Delta ABC\text{ và }\Delta DBE\text{ có:}\)
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BAC}=\widehat{BDE}=90^0\left(gt\right)\\BD=AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DBE\left(g-c-g\right)\)
\(c)\text{Xét }\Delta ABH\text{ và }\Delta DBH\text{ có:}\)
\(\left\{{}\begin{matrix}BD=AB\left(gt\right)\\BH\text{ chung}\\\widehat{BAH}=\widehat{BDH}=90^0\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABH=\Delta DBH\left(ch-gn\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{DBH}\left(\text{hai góc tương ứng}\right)\)
\(\Rightarrow BH\text{ là phân giác }\widehat{ABC}\)
\(d)\text{Mik k bt:< }\)
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A. AB>AC, M là điểm tuỳ ý trên cạnh BC. Qua M kẻ tia Mx vuông góc với BC và cắt AB tại I, cắt CA tại D. Chứng minh rằng
a.)Tam giác ABC đồng dạng với tam giác MDC
b.)BI.BA=BM.BC
a)xét tg ABC và tg MDC có: BAC=DMC=90, ^C chung
=>tg ABC đ.dạng vs tg MDC(g.g)
b)xét tg ABC và tg MBI có: CAB=BMI=90, ^B chung
=>tg ABC đ.dạng vs tg MBI(g.g) =>AB/MB=BC/BI=>AB.BI=BM.BC(đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,kẻ AD vuông góc với BC (D thuộc BC) cho tam giác ABC vuông tại A,kẻ AD vuông góc với BC (D thuộc BC).Trên đường thẳng vuông góc với BC tại C lấy điểm E sao cho CE=AD(E và A thuộc 2 mặt khác phía bờ chứa cạnh DC) Chứng minh rằng: a) tam giác ADC= tam giác ECD b) DE vuông góc AB c)CED=ABC Nhanh 10 phút nx MN ơi hình nx nhé
Đáp án:
Giải thích các bước giải:
Hình bạn tự vẽ nhé!!
a). Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD là cạnh chung
Góc ABD = góc EBD (đường phân giác BD)
=> tam giác ABD=tam giác EBD (cạnh huyền-góc nhọn)
b). Gọi I là giao điểm của BD và AE.
Xét tam giác ABI và tam giác EBI có:
AB=EB (tam giác ABD=tam giác EBD)
Góc ABI=góc EBI (đường phân giác BD)
BI là cạnh chung.
=> tam giác ABI=tam giác EBI (c.g.c)
=> AI=EI => I là trung điểm của AE. (1)
=> Góc BIA=góc BIE
Mà góc BIA+góc BIE=180 độ (hai góc kề bù)
=> góc BIA=góc BIE=90 độ.
=> BI vuông góc với AE (2).
Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AE
d). Xét tam giác ADF vuông tại A và tam giác EDC vuông tại E có:
AD=ED (tam giác ABD = tam giác EBD)
AF=CE (GT)
=> tam giác ADF=tam giác EDC (hai cạnh góc vuông)
=> Góc ADF = góc EDC
cho xin tích ạ
Đúng 2
Bình luận (0)
Giải thích các bước giải:
Hình bạn tự vẽ nhé!!
a). Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD là cạnh chung
Góc ABD = góc EBD (đường phân giác BD)
=> tam giác ABD=tam giác EBD (cạnh huyền-góc nhọn)
b). Gọi I là giao điểm của BD và AE.
Xét tam giác ABI và tam giác EBI có:
AB=EB (tam giác ABD=tam giác EBD)
Góc ABI=góc EBI (đường phân giác BD)
BI là cạnh chung.
=> tam giác ABI=tam giác EBI (c.g.c)
=> AI=EI => I là trung điểm của AE. (1)
=> Góc BIA=góc BIE
Mà góc BIA+góc BIE=180 độ (hai góc kề bù)
=> góc BIA=góc BIE=90 độ.
=> BI vuông góc với AE (2).
Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AE
d). Xét tam giác ADF vuông tại A và tam giác EDC vuông tại E có:
AD=ED (tam giác ABD = tam giác EBD)
AF=CE (GT)
=> tam giác ADF=tam giác EDC (hai cạnh góc vuông)
=> Góc ADF = góc EDC
Đúng 0
Bình luận (0)