Hentai
H SM spank thể loại
Những câu hỏi liên quan
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn
S
M
1
4
S
A
,
S
N
1
3
S
B
,
S
P
3
S
C
Thể tích của khối chóp S.MNP theo V A.
V
5
B.
V
4
C.
V
3
D. ...
Đọc tiếp
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn S M = 1 4 S A , S N = 1 3 S B , S P = 3 S C Thể tích của khối chóp S.MNP theo V
A. V 5
B. V 4
C. V 3
D. V 2
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn SM
1
4
SA, SN
1
3
SB, SP 3SC. Thể tích của khối chóp S.MNP theo V
A
.
V
5
B
.
V
4
C
.
V
3
D...
Đọc tiếp
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn SM = 1 4 SA, SN = 1 3 SB, SP = 3SC. Thể tích của khối chóp S.MNP theo V
A . V 5
B . V 4
C . V 3
D . V 2
Đáp án là B
Theo công thức tỉ số thể tích của hình chóp tam giác ta có
Đúng 0
Bình luận (0)
Tính thể tích khối chóp S.MNP biết
S
M
a
3
, ΔMNP đều, ΔSMN vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. A.
2
a
3
3
B.
3
2
a
3
4
C....
Đọc tiếp
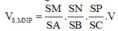
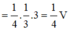
Tính thể tích khối chóp S.MNP biết S M = a 3 , ΔMNP đều, ΔSMN vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy.
A. 2 a 3 3
B. 3 2 a 3 4
C. 2 a 3 6
D. 3 2 a 3 2
Đáp án B
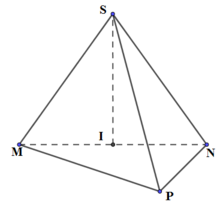
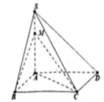
ΔSMN vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, gọi I là trung điểm của MN ⇒ SI⊥(ABC) và 
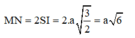
ΔMNP đều
Thể tích khối chóp S.MNP là
Đúng 0
Bình luận (0)
Cho hình chóp đều SABCD. Gọi M là trung điểm của BC. Góc giữa SM và (SBD) bằng 30 độ. Biết AB= a , Tính thể tích hình chóp SABCD
Gọi H là hình chiếu vuông góc của S lên đáy \(\Rightarrow\) H là tâm đáy
Gọi E là trung điểm BH \(\Rightarrow ME\perp BD\Rightarrow ME\perp\left(SBD\right)\)
\(\Rightarrow\widehat{MSE}=30^0\)
Ta có: \(ME=\dfrac{1}{2}CH\) (đường trung bình) \(=\dfrac{1}{4}AC=\dfrac{a\sqrt{2}}{4}\)
\(\Rightarrow SM=\dfrac{ME}{sin30^0}=\dfrac{a\sqrt{2}}{2}\) ; \(HM=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SM^2-HM^2}=\dfrac{a}{2}\)
\(V=\dfrac{1}{3}SH.AB^2=\dfrac{a^3}{6}\)
Đúng 2
Bình luận (0)
$triangle SAB, triangle SCD$ cân tại $S$. Kẻ trung tuyến $SM$ của $triangle SAB$, trung tuyến $SN$ của $triangle SCD Rightarrow SMperp AB, SNperp CD$$(SAB)cap(SCD)dparallel ABparallel CDRightarrow SMperp dRightarrow SMperp SNsubset(SCD)$$Rightarrow SM^2+SN^2MN^2AD^21$ (Pythagore)$dfrac{7}{10}S_{SAB}+S_{SCD}dfrac{1}{2}AB(SM+SN)Rightarrow SM+SNdfrac{7}{5}Rightarrow (SM+SN)^2dfrac{49}{25}Rightarrow SMcdot SNdfrac{12}{25}$Gọi $H$ là hình chiếu của $S$ lên $(ABCD)Rightarrow M,N,H$ thẳng h...
Đọc tiếp
$\triangle SAB, \triangle SCD$ cân tại $S$. Kẻ trung tuyến $SM$ của $\triangle SAB$, trung tuyến $SN$ của $\triangle SCD \Rightarrow SM\perp AB, SN\perp CD$
$(SAB)\cap(SCD)=d\parallel AB\parallel CD\Rightarrow SM\perp d\Rightarrow SM\perp SN\subset(SCD)$
$\Rightarrow SM^2+SN^2=MN^2=AD^2=1$ (Pythagore)
$\dfrac{7}{10}=S_{SAB}+S_{SCD}=\dfrac{1}{2}AB(SM+SN)\Rightarrow SM+SN=\dfrac{7}{5}\Rightarrow (SM+SN)^2=\dfrac{49}{25}\Rightarrow SM\cdot SN=\dfrac{12}{25}$
Gọi $H$ là hình chiếu của $S$ lên $(ABCD)\Rightarrow M,N,H$ thẳng hàng
$\triangle SMN$ vuông tại S có $SH$ là đường cao
$\Rightarrow \dfrac{1}{SH^2}=\dfrac{1}{SM^2}+\dfrac{1}{SN^2}\Rightarrow SH=\dfrac{SM\cdot SN}{\sqrt{SM^2+SN^2}}=\dfrac{12}{25}$
$\Rightarrow V_{S.ABCD}=\dfrac{4}{25}$
Cho hình chóp tam giác đều SABC Gọi M,N lần lượt là trung điểm của BC,SM Mặt phẳng (ABN) cắt SC tại E. Gọi
V
2
là thể tích của khối chóp
S
.
A
B
E
v
à
V
1
là thể tích khối chóp SABC Khẳng định nào sau đây đúng? A.
V
2
1
8
V...
Đọc tiếp
Cho hình chóp tam giác đều SABC Gọi M,N lần lượt là trung điểm của BC,SM Mặt phẳng (ABN) cắt SC tại E. Gọi V 2 là thể tích của khối chóp S . A B E v à V 1 là thể tích khối chóp SABC Khẳng định nào sau đây đúng?
A. V 2 = 1 8 V 1
B. V 2 = 1 4 V 1
C. V 2 = 1 3 V 1
D. V 2 = 1 6 V 1
Đáp án là C.
• Gọi I là trung điểm của EC.
Ta có I M // B E hay I M // N E .
Xét Δ S M I có N E // M I và N là trung điểm của SM suy ra E là trung điểm của SI .
Do đó S E = E I = I C ⇒ S E S C = 1 3 .
Ta có V S A B E V S A B C = S A S A . S B S B . S E S C = 1 3
.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình chữ nhật,
A
B
a
;
A
D
2
a
;
S
A
a
3
là điểm trên SA sao cho
S...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a ; A D = 2 a ; S A = a 3 là điểm trên SA sao cho S M = a 3 3 SA vuông góc với đáy. Tính thể tích của khối chóp S.MNC?
A. a 3 3 6
B. a 3 3 9
C. a 3 3 12
D. a 3 3 24
Đáp án: B
§ Hướng dẫn giải:
Ta có:
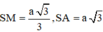
⇒ S M S A = 1 3
Ta có:
V S . B M C V S . B A C = S B S B = S M S A . S C S C = 1 3
⇒ V S . B M C = 1 3 V S . B A C = 1 6 V S . A B C D
Mà V S . A B C D = 1 3 S A . S A B C D = 2 a 3 3 3
⇒ V S . B C M = 1 6 V S . A B C D = a 3 3 9
Đúng 0
Bình luận (0)
Cho 2 đường thẳng ab và cd cắt nhau ở S. Sm là tia phân giác của góc aSc, Sn là tia đối của tia Sm. Chứng minh Sm là tia phân giác của góc bSc.
Cho tứ diện S.ABC trên đoạn thẳng SA, SB, SC lần lượt lấy các điểm M, N, P sao cho SM5MA SN2NB và SPkPC Kí hiệu
V
T
là thể tích của khối đa diện T. Biết rằng Tìm k?
Đọc tiếp
Cho tứ diện S.ABC trên đoạn thẳng SA, SB, SC lần lượt lấy các điểm M, N, P sao cho SM=5MA SN=2NB và SP=kPC Kí hiệu
V
T
là thể tích của khối đa diện T. Biết rằng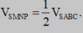 
Tìm k?
