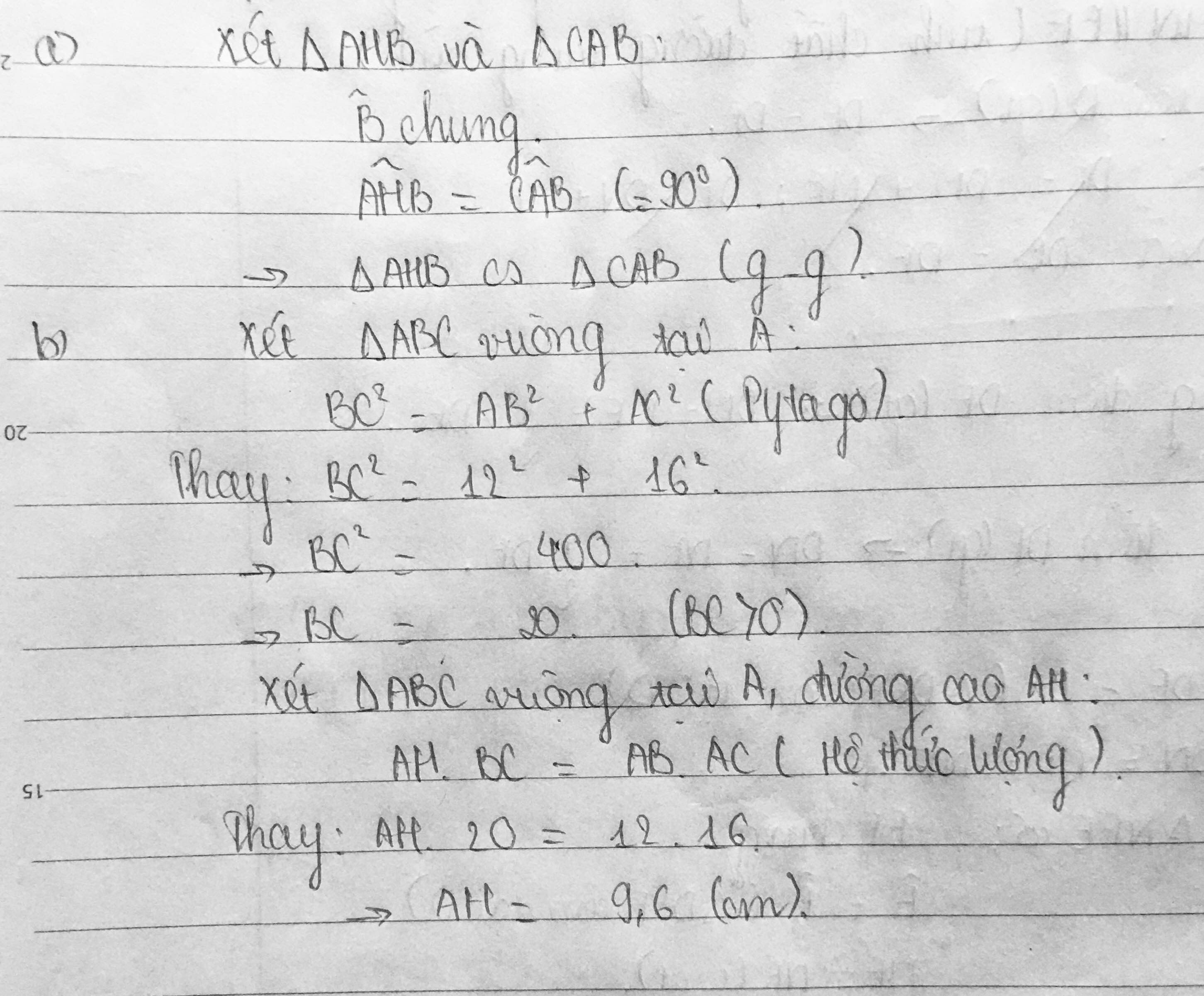Cho tam giác ABC cân tại B có AB =17 cm,AC = 16 cm. gọi M là trung điểm AC .tính BM

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. AB=17 cm, AC=16cm. Gọi Mlaf trung điểm của AC. Tính BM
Gọi M là trung điểm của AC nên AM = MC = 8 cm
Cho tam giác ABC cân tại B nên trung tuyến BM đồng thời là đường cao
Xét tg vuông ABM: AB^2 = AM^2 + MB^2
MB^2 = 17^2 - 8^2
MB^2 = 15^2
VẬY MB = 15 cm
______________________________________________________________
li-ke cho mk nhé bn Linh
Đúng 0
Bình luận (0)
Tam giác ABC cân tại A , AB=17 , AC=16 . Gọi M là trung điểm của AC . Tính BM
Tam giác ABC cân tại A =>AB=AC
Lại có AB= 17
AC=16
Từ 3 cái này suy ra sai đề
Đúng 0
Bình luận (0)
Cho tam giác ABC ( AB< AC). Trên AB lấy M, AC lấy N sao cho BM=CN. Gọi E là trung điểm của MN, F là trung điểm của BC, I là trung điểm BN.
a) CM tam giác IEF cân
b) Đường thẳng EF cắt AB, AC tại G và H. CM AG=AH
Câu 12: Cho tam giác ABC vuông tại C , có AB = 10 cm, AC cm = 6 . Trên tia đối của tia CB lấy D sao cho CD=CB .
a) Tính BC , so sánh góc A và góc B của tam giác ABC
b) Chứng minh tam giác ABD cân tại A.
c) Gọi M là trung điểm của AD , BM cắt AC tại G. Chứng minh GB +2GC>AB
d) Qua C kẻ CN DA / / sao cho N thuộc AB . Chứng minh D, G ,N thẳng hàng .
a: BC=8cm
BC>AC
=>góc A>góc B
b: XétΔABD có
AC vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
c: GB+2GC=GB+GA>AB
Đúng 0
Bình luận (0)
Bài 1. Cho tam giác ABC có AB cm 16 , BC cm 20 và AC cm 12 . a) Chứng minh : ABC vuông tại A . b) Gọi M là trung điểm của BC . KẻMFAC tại F . Chứng minh :FA FC . c) Gọi E là trung điểm của AB . Chứng minh : ME AB và tính độdài ME . Bài 2. Cho hình thang ABCD có hai đáy là AB và CD . Gọi E, F, K lần lượt là trung điểm các cạnh AD, BC, BD . a) Chứng minh: EK // AB ; KF // AB và E, F, K thẳng hàng. b) Gọi I là giao điểm EF và AC . Chứng minh : IA IC . c) Chứng minh : IE KF và KE IF. d) Ch...
Đọc tiếp
Bài 1. Cho tam giác ABC có AB cm 16 , BC cm 20 và AC cm 12 . a) Chứng minh : ABC vuông tại A . b) Gọi M là trung điểm của BC . KẻMFAC tại F . Chứng minh :FA = FC . c) Gọi E là trung điểm của AB . Chứng minh : ME AB và tính độdài ME . Bài 2. Cho hình thang ABCD có hai đáy là AB và CD . Gọi E, F, K lần lượt là trung điểm các cạnh AD, BC, BD . a) Chứng minh: EK // AB ; KF // AB và E, F, K thẳng hàng. b) Gọi I là giao điểm EF và AC . Chứng minh : IA = IC . c) Chứng minh : IE = KF và KE = IF. d) Cho biết AB 6 cm ; CD 10 cm . Tính IK.
Cho tam giác ABC có AB < AC. Lấy M thuộc AB, N thuộc AC sao cho BM = CN. Gọi I, K lần lượt là trung điểm của MN và BC. Đường thẳng IK cắt AB, AC tại E, F. CM: Tam giác AEF cân.
1/ Cho tam giác ABC vuông tại A có đường phân giác AD và đường trung tuyến BM vuông góc tại E. Gọi H là trung điểm AE. BE cắt AC tại K.a) Cm: tam giác BDK vuông cân tại Db) Cm : (AD/AC)2 2/92/ Cho tam giác ABC vuông cân tại có đường trung tuyến AM. Vẽ MH vuông AB ( H thuộc AB ). Từ A hạ AI vuông CH tại I. Gọi N là giao điểm IC và AM. BI cắt AC tại K.a) Cm: BI vuông với IM tại Ib) Cm: AN.AB IC.MK
Đọc tiếp
1/ Cho tam giác ABC vuông tại A có đường phân giác AD và đường trung tuyến BM vuông góc tại E. Gọi H là trung điểm AE. BE cắt AC tại K.
a) Cm: tam giác BDK vuông cân tại D
b) Cm : (AD/AC)2 = 2/9
2/ Cho tam giác ABC vuông cân tại có đường trung tuyến AM. Vẽ MH vuông AB ( H thuộc AB ). Từ A hạ AI vuông CH tại I. Gọi N là giao điểm IC và AM. BI cắt AC tại K.
a) Cm: BI vuông với IM tại I
b) Cm: AN.AB = IC.MK
Cho tam giác ABC vuông tại A, đường cao AH. a, Chứng minh tam giác AHB đồng dạng với tam giác CAB b, Cho AB=12 cm, AC=16 cm. Tính độ dài AH? c, Kẻ DH vuông góc với AC tại D. Gọi M là trung điểm của AB; CM cắt HD tại I. Chứng minh I là trung điểm của HD
Cho tam giác ABC vuông cân tại A. Trên cạnh AC lấy M bất kì (M khác A,C) . Trên cạnh AB lấy E sao cho AE=CM. Gọi O là trung điểm cạnh BC
a, CM tam giác OEM vuông cân
b, Đường thẳng qua A và song song với ME, cắt tia BM tại N. Chứng minh CN _|_ AC
c, Gọi H là giao điểm của OM và AN. Chứng minh rằng tích AH.AN không phụ thuộc vào vị trí M trên cạnh AC