cho tam giác ABC vuông tại A, và hình vuông BCDE. cm AB+AC<=CE

Những câu hỏi liên quan
cho tam giác ABC vuông tại A và hình vuông BCDE . cm AB+AC<CE
Xét tam giác BAC có :
BA+AC=BC(cạnh huyền của tam giác vuông)
Mà : BC+BE=EC(cạnh huyền của tam giác vuông)
Vậy suy ra : AB+AC<CE
Đúng 0
Bình luận (0)
chứng minh AB+AC nhỏ hơn hoặc bằng CE
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
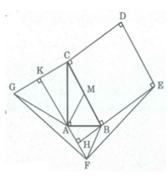
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )
Đúng 0
Bình luận (0)
cho tam giác ABC là tam giác vuông tại A và AB < AC. Vẽ hình vuông BCDE dựng ra phía ngoài của tam giác. G nằm trên AC sao cho AGE= 90 độ, F nằm trên EG sao cho BFE= 90 độ.
CMR: ABFG là hình vuông
Cho tam giác ABC nhọn (AB<AC) nội tiếp (O) có 2 đường cao BE, CE (D thuộc AC, E thuộc AB) và đường phân giác AS cắt (O) tại T (S thuộc BC, T khác A), DE cắt BC tại K
a) Cm BCDE nội tiếp, xác đinh tâm I của đtr ngoại tiếp tứ giác BCDE. Cm góc CKD=ABC-ACB
b) Cm KB.KC=KE.KD và TB2=TS.TA
c) Kẻ TV vuông góc với AB tại V. Cm IV vuông góc với AT
Cho tam giác ABC vuông tại A . Kẻ đường cao AH . Trên tia Hx vuông góc với AB , lấy điểm D sao cho AB là đường trung trực của đt HD . Trên tia Hy vuông góc với AC lấy điểm E sao cho AC là đường trung trực của HE
a) CM ba điểm D,E,A thẳng hàng
b ) CM tứ giác BCDE là hình thang vuông
a: Ta có: H và D đối xứng với nhau qua AB
nên AH=AD; BH=BD
=>ΔHAD cân tại A
=>AB là phân giác của góc HAD(1)
Ta có H và E đối xứngvới nhau qua AC
nên AH=AE; CH=CE
=>ΔAHE cân tại A
=>AC là phân giác của góc HAE(2)
Từ (1) và (2) suy ra góc DAE=2xgóc BAC=180 độ
=>D,A,E thẳng hàng
b: Xét ΔAHB và ΔADB có
AH=AD
BH=BD
AB chung
Do đó: ΔAHB=ΔADB
Suy ra: góc ADB=90 độ
=>BD vuông góc với DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
HC=EC
AC chung
Do đó: ΔAHC=ΔAEC
Suy ra: góc AEC=90 độ
=>CE vuông góc với ED(4)
Từ (3) và (4) suy ra BDEC là hình thang vuông
c: ED=AE+AD
=AH+AH=2AH
d: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
Do đó: ΔDHE vuông tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính diện tích tứ giác DEFG
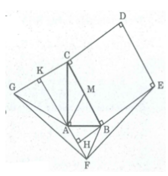
S B C D E = B C 2 = 2 a 2 = 4 a 2 (dvdt)
Trong tam giác vuông BHA, theo Pi-ta-go, ta có: A H 2 + B H 2 = A B 2
⇒ B H 2 = A B 2 - A H 2 = a 2 - a 2 / 4 = 3 a 2 / 4 ⇒ BH = (a 3 )/2
S
A
B
F
= 1/2 BH.FA = 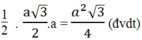
Trong tam giác vuông AKG, theo Pi-ta-go, ta có: A C 2 = A K 2 + K C 2
⇒ A K 2 = A C 2 - K C 2 = 3 a 2 - 3 a 2 / 4 = 9 a 2 / 4 ⇒ AK = 3a/2 (đvdt)
S
A
C
G
= 1/2 AK.CG = 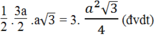
S D E F G = S B C D E + S F B E + S FAB + S F A G + S A C G + S A B C
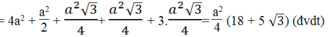
Đúng 0
Bình luận (0)
1) cho tam giác ABC vuông tại A (AB<AC) AM là trung tuyến. Trên dường thẳng AM lấy D sao cho MA = Md
a) CM tứ giác ABCD là hình chữ nhật
b) Gọi E là điểm đối xứng của A giữa BC.Cm AE vuông ED
c)CM tứ giác BCDE là hình thang cân
1. Cho tam giác ABC vuông tại A có AB 9 cm , BC 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,2. Cho tam giác ABC vuông tại A có AC 5 cm , AB 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH . 3. Cho tam giác ABC vuông tại A có BC 40 cm , AC 36 cm . Tính AB , BH , CH và AH ,4. Cho tam giác ABC vuông tại A có BC 24 cm . Tính AB , AC , cho biết 2 AB -AC .5. Cho tam giác ABC vuông tại A có AH là đường cao . BH 10 cm ,...
Đọc tiếp
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)
Đúng 1
Bình luận (0)
1. Cho tam giác ABC vuông tại A có AB 9 cm , BC 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,2. Cho tam giác ABC vuông tại A có AC 5 cm , AB 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH . 3. Cho tam giác ABC vuông tại A có BC 40 cm , AC 36 cm . Tính AB , BH , CH và AH ,4. Cho tam giác ABC vuông tại A có BC 24 cm . Tính AB , AC , cho biết 2 AB -AC .5. Cho tam giác ABC vuông tại A có AH là đường cao . BH 10 cm ,...
Đọc tiếp
1. Cho tam giác ABC vuông tại A có AB = 9 cm , BC = 15 cm , AH là đường C10 ( H thuộc cạnh BC ) . Tính BH , CH , AC và AH ,
2. Cho tam giác ABC vuông tại A có AC = 5 cm , AB = 4 cm . Tính : a ) Cạnh huyền BC . b ) Hình chiếu của AB và AC trên cạnh huyền . c ) Đường cao AH .
3. Cho tam giác ABC vuông tại A có BC = 40 cm , AC = 36 cm . Tính AB , BH , CH và AH ,
4. Cho tam giác ABC vuông tại A có BC = 24 cm . Tính AB , AC , cho biết 2 AB = -AC .
5. Cho tam giác ABC vuông tại A có AH là đường cao . BH = 10 cm , CH = 42 cm . Tính BC , AH , AB và AC ,
6. Cho đường tròn tâm O bán kính R = 10 cm . A , B là hai điểm trên đường tròn ( O ) và I là trung điểm của đoạn thẳng AB . a ) Tính AB nếu OI = 7 cm . b ) Tính OI nếu AB = 14 cm .













