trong mặt phẳng tọa độ Oxy, cho 2 đường cong thỏa mãn:
(C1) x2+y2-6x-8y+16 = 0
(C2) x2+y2+6x-6y+14 = 0
Tìm tọa độ của
M thuộc C1
N thuộc C2
K thuộc Ox
sao cho KM+KN đạt giá trị min
Những câu hỏi liên quan
trong mặt phẳng tọa độ Oxy, cho 2 đường cong thỏa mãn:
(C1) x2+y2-6x-8y+16 = 0
(C2) x2+y2+6x-6y+14 = 0
Tìm tọa độ của \(\left\{{}\begin{matrix}M\in C1\\N\in C2\\K\in Ox\end{matrix}\right.\)
sao cho KM+KN đạt giá trị min
Trong hệ tọa độ Oxy, cho hai đường tròn có phương trình (C1) : x2+ y2- 4y -5 0 và (C2) : x2+ y2- 6x + 8y +16 0 . Phương trình nào sau đây là tiếp tuyến chung của 2 đường tròn. D. Đáp án khác.
Đọc tiếp
Trong hệ tọa độ Oxy, cho hai đường tròn có phương trình (C1) : x2+ y2- 4y -5 = 0 và (C2) : x2+ y2- 6x + 8y +16= 0 . Phương trình nào sau đây là tiếp tuyến chung của 2 đường tròn.
D. Đáp án khác.
Đáp án D
- Ta có :
(C1) tâm I1(0;2) và R1= 3; (C2) tâm I2( 3;-4) và R2= 3
- Nhận xét : 
không cắt C2
- Gọi d: ax+ by+ c= 0 là tiếp tuyến chung , thế thì : d(I1; d) = R1 và d (I2; d) = R2
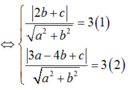
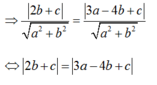
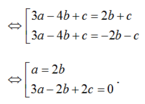
- Trường hợp: a= 2b thay vào (1):
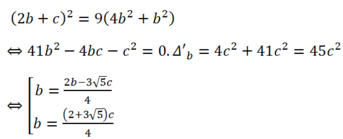
- Do đó ta có hai đường thẳng cần tìm :
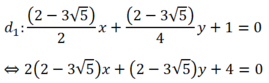
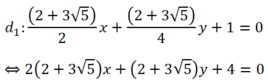
- Trường hợp :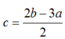 
thay vào :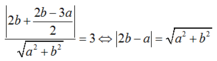 
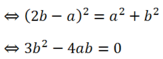
-Có 2 đường thẳng : d3: 2x- 1 = 0 và d4: 6x + 8y -1= 0.
Có tất cả 4 tiếp tuyến chung.
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn
C
1
:
x
2
+
y
2
−
2
x
−
2
y
−
2
0
và
C
2
:
x
2
+
y
2
+
12...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn C 1 : x 2 + y 2 − 2 x − 2 y − 2 = 0 và C 2 : x 2 + y 2 + 12 x − 16 y = 0. Phép đồng dạng F tỉ số k biến C 1 thành C 2 Tìm k ?
A. k = 1 5
B. k= -6
C. k= 2
D. k= 5
Đáp án D
Ta có:
C 1 : x − 1 2 + y − 1 2 = 4 ⇒ R 1 = 2 ; C 2 : x + 6 2 + y − 8 2 = 100 ⇒ R 2 = 10
⇒ k = R 2 R 1 = 10 2 = 5.
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn
C
1
:
x
2
+
y
2
−
2
x
−
2
y
−
2
0
và
C
2
:
x
2
+
y
2
+
12...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn C 1 : x 2 + y 2 − 2 x − 2 y − 2 = 0 và C 2 : x 2 + y 2 + 12 x − 16 y = 0 . Phép đồng dạng F tỉ số k biến C 1 thành C 2 . Tìm k?
A. k = 1 5
B. k = − 6
C. k = 2
D. k = 5
Đáp án D
Ta có:
C 1 : x − 1 2 + y − 1 2 = 4
⇒ R 1 = 2 ; C 2 : x + 6 2 + y − 8 2 = 100 ⇒ R 2 = 10
k = R 1 R 2 = 10 2 = 5
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn
C
1
:
x
2
+
y
2
-
2
x
-
2
y
-
2
0
và
C
2...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn C 1 : x 2 + y 2 - 2 x - 2 y - 2 = 0 và C 2 : x 2 + y 2 + 12 x - 16 y = 0 . Phép đồng dạng F tỉ số k biến C 1 thành C 2 . Tìm k?
A. 1 5
B. -6
C. 2
D. 5
Trong mặt phẳng tọa độ Oxy, cho đường tròn
C
1
:
x
2
+
y
2
4
,
C
2
:
x
2
+
y
2
-
12
x
+
18
0
và đường thẳng...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn C 1 : x 2 + y 2 = 4 , C 2 : x 2 + y 2 - 12 x + 18 = 0 và đường thẳng d : x - y + 4 = 0 . Phương trình đường tròn có tâm thuộc C 2 , tiếp xúc với d và cắt C 1 tại hai điểm phân biệt A và B sao cho AB vuông góc với d là:
A. x - 3 2 + y - 3 2 = 4
B. x - 3 2 + y - 3 2 = 8
C. x + 3 2 + y + 3 2 = 8
D. x + 3 2 + y + 3 2 = 4
Trong mặt phẳng tọa độ Oxy, cho đường tròn
(
C
2
)
:
x
2
+
y
2
-
12
x
+
18
0
và đường thẳng d:x-y+4. Phương trình đường tròn có tâm thuộc (
C
2
), tiếp xúc với d và cắt (
C
1
) tại hai điểm phân biệt A và B sao c...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn ( C 2 ) : x 2 + y 2 - 12 x + 18 = 0 và đường thẳng d:x-y+4. Phương trình đường tròn có tâm thuộc ( C 2 ), tiếp xúc với d và cắt ( C 1 ) tại hai điểm phân biệt A và B sao cho AB vuông góc với d là
Cho hai đường tròn
C
1
:
x
2
+
y
2
−
6
x
−
4
y
+
9
0
v
à
C
2
:
x
2
+
y
2
−
2
x
−
8
y
+...
Đọc tiếp
Cho hai đường tròn C 1 : x 2 + y 2 − 6 x − 4 y + 9 = 0 v à C 2 : x 2 + y 2 − 2 x − 8 y + 13 = 0 . Giao điểm của hai đường tròn là
A.A(1; 3), B(2; 4)
B.A(1; 2), B(3; 4)
C.A(1; 4), B(2; 3)
D. Không tồn tại
Tọa độ giao điểm là nghiệm của hệ phương trình
x 2 + y 2 − 6 x − 4 y + 9 = 0 x 2 + y 2 − 2 x − 8 y + 13 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 − 4 x + 4 y − 4 = 0 ⇔ x 2 + y 2 − 6 x − 4 y + 9 = 0 ( 1 ) x − y + 1 = 0 ( 2 )
Từ (2) suy ra: y = x+ 1 thay vào (1) ta được:
x 2 + ( x + 1 ) 2 - 6 x – 4 ( x + 1 ) + 9 = 0 x 2 + x 2 + 2 x + 1 - 6 x - 4 x – 4 + 9 = 0
2 x 2 – 8 x + 6 = 0
Vậy 2 đường tròn đã cho cắt nhau tại 2 điểm là (1; 2) và (3;4).
ĐÁP ÁN B
Đúng 0
Bình luận (0)
Số tiếp tuyến chung của hai đường tròn
(
C
1
)
:
x
2
+
y
2
-
2
x
+
4
y
+
1
0
v
à
(
C
2
)
:
x
2
+
y
2
+
6
x
-
8
y
+
20
0...
Đọc tiếp
Số tiếp tuyến chung của hai đường tròn ( C 1 ) : x 2 + y 2 - 2 x + 4 y + 1 = 0 v à ( C 2 ) : x 2 + y 2 + 6 x - 8 y + 20 = 0
A. 1
B. 2
C. 3
D. 4
