Trong các hình chữ nhật nội tiếp trong hình tròn bán kính 3cm, tìm hình có diện tích lớn nhất

Những câu hỏi liên quan
Trong các hình chữ nhật nội tiếp trong hình tròn bán kính 3cm, tìm hình có diện tích lớn nhất.
Gọi x là độ dài cạnh hình chữ nhật không nằm trên đường kính đường tròn 0<x<10.
Khi đó độ dài cạnh hình chữ nhật nằm trên đường tròn là:
Diện tích hình chữ nhật:
Đặt
Ta có:
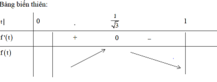
Lập bảng biến thiên ta thấy hàm số f(x) đạt giá trị lớn nhất tại .
Vậy diện tích lớn nhất của hình chữ nhật là:
Đúng 0
Bình luận (0)
Tính diện tích lớn nhất
S
max
của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính
R
6
c
m
nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp. A.
S
max
36
π
c
m
2
B.
S
max
36...
Đọc tiếp
Tính diện tích lớn nhất S max của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R = 6 c m nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp.

A. S max = 36 π c m 2
B. S max = 36 c m 2
C. S max = 96 π c m 2
D. S max = 18 c m 2
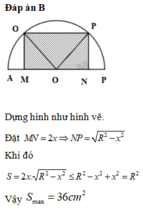
Đáp án B
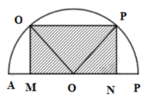
Dựng hình như hình vẽ. Đặt M N = 2 x ⇒ N P = R 2 − x 2
Khi đó S = 2 x . R 2 − x 2 ≤ R 2 − x 2 + x 2 = R 2
Vậy S max = 36 c m 2
Đúng 0
Bình luận (0)
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán kính 10cm (hình vẽ) A.
160
c
m
2
B.
100
c
m
2
C.
80
c
m
2
D.
200
c
m
2
Đọc tiếp
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán kính 10cm (hình vẽ)
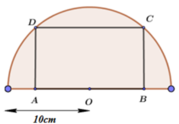
A. 160 c m 2
B. 100 c m 2
C. 80 c m 2
D. 200 c m 2
Tính diện tích lớn nhất của hình chữ nhật ABCD nội tiếp trong nửa đường tròn có bán kính 10cm (hình vẽ)
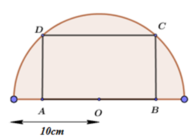
A. 160
B. 100
C. 80
D. 200
Tính diện tích lớn nhất
S
m
a
x
của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R 6 cm nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp A.
S
m
a
x
...
Đọc tiếp
Tính diện tích lớn nhất S m a x của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R = 6 cm nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp

A. S m a x = 36 πcm 2
B. S m a x = 36 c m 2
C. S m a x = 96 πcm 2
D. S m a x = 18 c m 2
Chứng minh rằng trong các hình chữ nhật nội tiếp hình tròn bán kính R thì hình vuông là hình có chu vi lớn nhất và có diện tích lớn nhất.
Đây ko phải toán lớp 6 mà là toán nâng cao của lớp 8,9
Đúng 0
Bình luận (0)
Nhà bác An có một khoảng đất trống phía trước nhà là nửa đường tròn bán kính R1m bác muốn trồng hoa trên diện tích là hình chữ nhật nội tiếp trong nửa đường tròn sao cho một cạnh của hình chữ nhật nằm dọc theo đường kính của đường tròn . Tính diện tích lớn nhất của mảnh đất trồng hoa. A.
S
m
a
x
0
,
5
m
2...
Đọc tiếp
Nhà bác An có một khoảng đất trống phía trước nhà là nửa đường tròn bán kính R=1m bác muốn trồng hoa trên diện tích là hình chữ nhật nội tiếp trong nửa đường tròn sao cho một cạnh của hình chữ nhật nằm dọc theo đường kính của đường tròn . Tính diện tích lớn nhất của mảnh đất trồng hoa.
A. S m a x = 0 , 5 m 2
B. S m a x = 2 m 2
C. S m a x = 1 m 2
D. S m a x = 0 , 75 m 2
Đáp án C
Giả sử khoảng đất được mô phỏng như hình vẽ. Mảnh vườn trồng hoa là AMNB
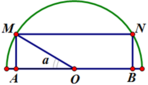
Khi đó R=OM=1m.
Gọi a = M O A ^ . Ta có MA=OM.sin a(m) và AB=2AO=2OM.cos a=2cos a(m).
Diện tích mảnh đất trồng hoa là S A M N B = M A . A B = 2 sin a cos a = sin 2 a ≤ 1 .
Vậy diện tích mảnh đất trồng hoa lớn nhất bằng 1( m 2 ) khi 2 a = 90 ° ⇔ a = 45 °
Đúng 0
Bình luận (0)
Trong các hình sau đây, hình nào có diện tích lớn nhất ?
a. Hình tròn có bán kính 2cm
b. Hình vuông có độ dài cạnh 3,5cm
c. Tam giác với độ dài các cạnh là 3cm, 4cm, 5cm
d. Nửa mặt cầu bán kính 4cm
a) Hình tròn có bán kính 2cm có diện tích : S = π. 2 2 = 4π ( c m 2 )
b) Hình vuông có độ dài cạnh 3,5cm có diện tích : S = 3 , 5 2 = 12,25 ( c m 2 )
c) tam giác có các cạnh 3cm,4cm,5cm nên nó là tam giác vuông
Khi đó tam giác có diện tích: S =(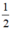 ).3.4 =6(
c
m
2
)
).3.4 =6(
c
m
2
)
d) Nửa mặt cầu bán kính 4cm có diện tích : S= (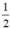 ).4.
π
.
4
2
= 32
π
(
c
m
2
)
).4.
π
.
4
2
= 32
π
(
c
m
2
)
Vậy trong các hình trên thì nửa mặt cầu bán kính 4cm có diện tích lớn nhất
Vậy chọn đáp án (D)
Đúng 0
Bình luận (0)
Trong tát cả các hình nón nội tiếp hình cầu bán kính R , hình nón có diện tích xung quanh lớn nhất khi A.
h
2
R
3
B.
h
4
R
3
C.
h
5
R...
Đọc tiếp
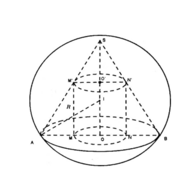
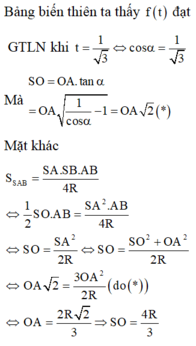
Trong tát cả các hình nón nội tiếp hình cầu bán kính R , hình nón có diện tích xung quanh lớn nhất khi
A. h = 2 R 3
B. h = 4 R 3
C. h = 5 R 3
D. h = R