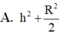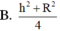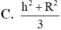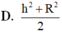Các câu hỏi tương tự
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
Đọc tiếp
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
![]()
![]()
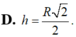
Cho hình nón có bán kính đáy r 1, chiều cao h
3
. Tính diện tích xung quanh
S
x
q
của hình nón đó.
Đọc tiếp
Cho hình nón có bán kính đáy r = 1, chiều cao h = 3 . Tính diện tích xung quanh S x q của hình nón đó.
![]()
![]()
![]()
![]()
Cho hình cầu (S) tâm I, bán kính R không đổi. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp hình cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất A. h
R
2
B. h R C. h
R
2
D. h
R
2
2
Đọc tiếp
Cho hình cầu (S) tâm I, bán kính R không đổi. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp hình cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất
A. h = R 2
B. h =R
C. h = R 2
D. h = R 2 2
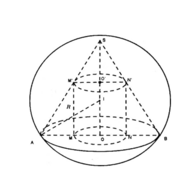
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kì nội tiếp mặt cầu (S) (tham khảo hình vẽ bên). Thể tích khối nón (H) là
V
1
; thể tích phần còn lại là
V
2
. Giá trị lớn nhất của
V
1
V
2
bằng A. ...
Đọc tiếp
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kì nội tiếp mặt cầu (S) (tham khảo hình vẽ bên). Thể tích khối nón (H) là V 1 ; thể tích phần còn lại là V 2 . Giá trị lớn nhất của V 1 V 2 bằng

A. 76 32
B. 81 32
C. 32 76
D. 32 81
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kỳ nội tiếp mặt cầu (S) Thể tích khối nón (H) là
V
1
thể tích phần còn lại của khối cầu là
V
2
Giá trị lớn nhất của
V
1
V
2
bằng: A.
81
32
B.
76
32...
Đọc tiếp
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kỳ nội tiếp mặt cầu (S) Thể tích khối nón (H) là V 1 thể tích phần còn lại của khối cầu là V 2 Giá trị lớn nhất của V 1 V 2 bằng:
A. 81 32
B. 76 32
C. 32 81
D. 32 76
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có
B
A
C
^
75
0
,
A
C
B
^
60
0
. Kẻ BH
⊥
AC. Quay quanh AC thì
∆
BHC tạo...
Đọc tiếp
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 0 , A C B ^ = 60 0 . Kẻ BH ⊥ AC. Quay quanh AC thì ∆ BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R.
A. 3 + 2 2 2 πR 2
B. 3 + 2 3 2 πR 2
C. 3 ( 1 + 2 ) 4 πR 2
D. 3 ( 1 + 3 ) 4 πR 2
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N).
S
x
q
,
S
t
p
,
V
lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A
.
V
1...
Đọc tiếp
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). S x q , S t p , V lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A . V = 1 3 πrh
B . l 2 = h 2 + r 2
C . S t p = πr ( 1 + r )
D . S x q = πrl
Một hình nón có bán kính đáy r a, chiều cao h 2a
2
. Diện tích toàn phần của hình nón được tính theo a là
Đọc tiếp
Một hình nón có bán kính đáy r = a, chiều cao h = 2a 2 . Diện tích toàn phần của hình nón được tính theo a là
![]()
![]()
![]()
![]()
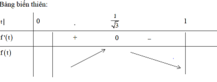
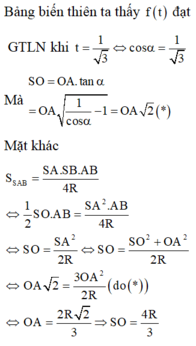
Cho hình nón có đỉnh S, chiều cao h và bán kính đáy bằng R. Mặt phẳng qua S cắt hình nón tạo ra một thiết diện tam giác. Diện tích lớn nhất của thiết diện bằng:
Đọc tiếp
Cho hình nón có đỉnh S, chiều cao h và bán kính đáy bằng R. Mặt phẳng qua S cắt hình nón tạo ra một thiết diện tam giác. Diện tích lớn nhất của thiết diện bằng: