Đáp án D
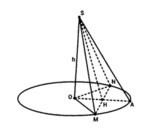
Thiết diện là tam giác SMN cân tại S.
Kẻ bán kính OA của hình nón
vuông góc với MN tại H


Đáp án D

Thiết diện là tam giác SMN cân tại S.
Kẻ bán kính OA của hình nón
vuông góc với MN tại H


Cho hình nón tròn xoay có chiều cao h = 20 cm, bán kính đáy r = 25 cm.. Mặt phẳng ( α ) đi qua đỉnh của hình nón cách tâm của đáy 12 cm Tính diện tích thiết diện của hình nón cắt bởi mặt phẳng ( α ) .
A. S = 400 ( c m 2 )
B. S = 406 ( c m 2 )
C. S = 300 ( c m 2 )
D. S = 500 ( c m 2 )
Cho hình nón tròn xoay có đường cao h = 40 (cm), bán kính đáy r = 50 (cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 (cm). Tính diện tích của thiết diện
A. S = 800 c m 2
B. S = 1200 c m 2
C. S = 1600 c m 2
D. S = 2000 c m 2
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x, 0 < x <h. (C ) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất
A. h 2
B. h 2 2
C. h 3 2
D. h 3
Cho hình nón có chiều cao bằng 2. Gọi ( α ) là mặt phẳng đi qua đỉnh S của hình nón và cắt mặt đáy hình nón theo một dây cung AB và tạo với đáy hình nón một góc π 4 . Tính diện tích của mặt cắt SAB. Biết dây cung AB có số đo 2 π 3 .
A . 4 6
B . 2 6
C . 4 3
D . 4 2
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm O 1 ( O 1 nằm giữa O và O') cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích bằng nhau
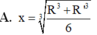
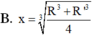
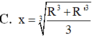
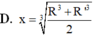
Cho hình nón đỉnh S và O là tâm đáy. Thiết diện qua trục của hình nón là một tam giác cân có đường cao h=3cm biết hai cạnh bên dài gấp đôi cạnh đáy. Tính diện tích xung quanh của hình nón đó.
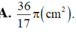
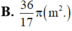
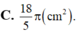

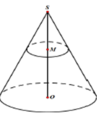
Một hình nón có chiều cao SO=50cm và có bán kính đáy bằng 10cm Lấy điểm M thuộc đoạn SO sao cho OM=20cm Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
![]()
![]()
![]()
![]()
Một hình nón có bán kính đáy bằng 1 và có thiết diện qua trục là một tam giác vuông cân. Tính diện tích xung quanh của hình nón.
![]()
![]()
![]()
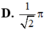
Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng a, diện tích xung quanh của hình nón là:
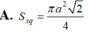
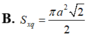
![]()
![]()