cho tam giác abc vuông tại a,ah là đường cao ứng với cạnh huyền của tam giác.biết ch=4cm,hb=16cm.tính độ dài ah,ab,ac

Những câu hỏi liên quan
cho tam giác abc vuông tại a.ah là đường cao ứng với cạnh huyền của tam giác.biết ch=4cm,hb=16cm.tính độ daif ah,ab,ac
Cho tam giác ABC vuông tại A có đường cao AH.Biết AC=15cm; HB=16cm.Tính BC;AB;AH;CH
Ta có: \(AC^2=CH\cdot BC\)
\(\Leftrightarrow CH^2+16HC-225=0\)
\(\Leftrightarrow CH^2+25HC-9HC-225=0\)
\(\Leftrightarrow CH=9\left(cm\right)\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=15^2-9^2=144\)
hay AH=12cm
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20cm
Ta có: BC=BH+HC
nên BC=9+16=25cm
Đúng 0
Bình luận (0)
1/cho tam giác abc vuông tại a đường cao AH=2cm,AB=1/2AC. tính AB,AC,HB,HC
2/cho tam giác abc vuông tại a đường cao AH=12cm.tính cạnh huyền BC,biết \(\dfrac{HB}{HC}\)=\(\dfrac{1}{3}\)
Bài 2:
Ta có: \(\dfrac{HB}{HC}=\dfrac{1}{3}\)
nên HC=3HB
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB^2=48\)
\(\Leftrightarrow HB=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\cdot HB=16\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
Bài 1:
ta có: \(AB=\dfrac{1}{2}AC\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{1}{4}\)
\(\Leftrightarrow HC=4HB\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=1\left(cm\right)\)
\(\Leftrightarrow HC=4\left(cm\right)\)
hay BC=5(cm)
Xét ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=HC\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Bài 7. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, trung tuyến AM. Biết rằng AH = 4,8cm,
AM = 5cm. Tính độ dài cạnh AC?
Bài 8. Đường trung tuyến ứng với cạnh huyền của một tam giác vuông dài 25cm. Tỉ số hai hình chiếu của
hai cạnh góc vuông trên cạnh huyền là 16 : 9. Tính độ dài hai cạnh góc vuông
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6 cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4 và HC = 6 a) tính độ dài AH, AB, AC b) Gọi M là trung điểm của AC. Tính số đo góc AMB ( làm tròn đến độ)
a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (0)
1, Cho tam giác ABC ( góc A90 độ). Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với cạnh huyền BC tại D. C/m: BD^2-CD^2AB^22, Cho tam giác ABC( góc A90 độ). phân giác AD, đường cao AH. biết BD15cm, CD20cm, tính BH, CH3, Cho tam giác ABC( góc A90 độ). AB12cm, AC16cm, phân giác AD, đường cao AH. tính HB,HC,HD4, Cho tam giác ABC( góc A90 độ) đường cao AH. Tính chu vi tam giác ABC biết AH 14 cm, HB/HC1/4giúp đỡ mình nhé, mình đang cần gấp
Đọc tiếp
1, Cho tam giác ABC ( góc A=90 độ). Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với cạnh huyền BC tại D. C/m: BD^2-CD^2=AB^2
2, Cho tam giác ABC( góc A=90 độ). phân giác AD, đường cao AH. biết BD=15cm, CD=20cm, tính BH, CH
3, Cho tam giác ABC( góc A=90 độ). AB=12cm, AC=16cm, phân giác AD, đường cao AH. tính HB,HC,HD
4, Cho tam giác ABC( góc A=90 độ) đường cao AH. Tính chu vi tam giác ABC biết AH= 14 cm, HB/HC=1/4
giúp đỡ mình nhé, mình đang cần gấp
3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông lại A , đường cao AH chia cạnh huyền thành hai đoạn, BH CH có độ dài lẩn lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của Htrên AB và AC .a) Tính độ dài AH . Từ đó suy ra độ dài của DE .b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N .Chứng minh M là trung điểm của BH và N là trung điểm của CH .c) Tính diện tích tứ giác DENM .Giúp mình nhanh với mn ơi, mai phải nộp rồi.
Đọc tiếp
Cho tam giác ABC vuông lại A , đường cao AH chia cạnh huyền thành hai đoạn
, BH CH có độ dài lẩn lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H
trên AB và AC .
a) Tính độ dài AH . Từ đó suy ra độ dài của DE .
b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N .
Chứng minh M là trung điểm của BH và N là trung điểm của CH .
c) Tính diện tích tứ giác DENM .
Giúp mình nhanh với mn ơi, mai phải nộp rồi.
Cho tam giác vuông ABC vuông tại A, cạnh AB=5cm,AC=12cm.Từ trung điểm M của cạnhBCkẻ dường thẳng vuông góc vớiBC cắt cạnh góc vuông tại N .tính độ dài MN
Gọi AH là đường cao thuộc cạnh huyền (HϵBC).Tính AH,BH,CH
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13(cm)
Xét ΔMBN vuông tại M và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔMBN\(\sim\)ΔABC(g-g)
Suy ra: \(\dfrac{MN}{AC}=\dfrac{BM}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MN=\dfrac{BM\cdot AC}{AB}=\dfrac{6.5\cdot12}{6}=6.5\cdot2=13\left(cm\right)\)
Đúng 0
Bình luận (0)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot CB=AB\cdot AC\)
\(\Leftrightarrow AH\cdot13=5\cdot12=60\)
hay \(AH=\dfrac{60}{13}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow BH^2=5^2-\left(\dfrac{60}{13}\right)^2=\dfrac{625}{169}\)
hay \(BH=\dfrac{25}{13}\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên \(CH=BC-BH=13-\dfrac{25}{13}=\dfrac{144}{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
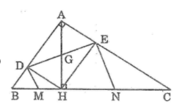
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Tính độ dài đoạn thẳng DE
![]()
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật
Suy ra: AH = DE (tính chất hình chữ nhật)
Tam giác ABC vuông tại A và có AH là đường cao
Theo hệ thức giữa đường cao và hình chiếu ta có:
A H 2 = HB.HC = 4.9 = 36 ⇒ AH = 6 (cm)
Vậy DE = 6 (cm)
Đúng 1
Bình luận (0)












