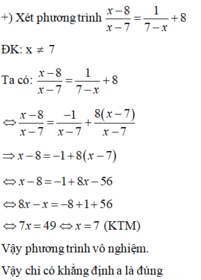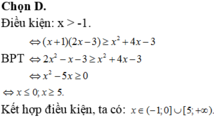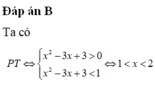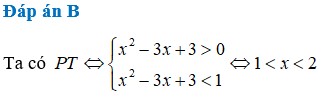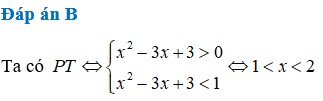tập nghiệm của bất phương trình x2 + 4x + 3≥0

Những câu hỏi liên quan
Tập nghiệm của hệ bất phương trình
x
2
-
4
x
+
3
0
x
2
-
6
x...
Đọc tiếp
Tập nghiệm của hệ bất phương trình x 2 - 4 x + 3 > 0 x 2 - 6 x + 8 > 0 là:
A.( - ∞ ;1) ∪ (3; + ∞ )
B.( - ∞ ;1) ∪ (4; + ∞ )
C. ( - ∞ ;2) ∪ (3; + ∞ )
D. (1;4)
Chọn B.
Ta có:
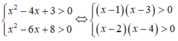
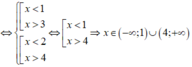
Vậy tập nghiệm của bất phương trình là S = ( - ∞ ;1) ∪ (4; + ∞ ).
Đúng 0
Bình luận (0)
Tập nghiệm của hệ bất phương trình
x
2
-
4
x
+
3
0
x
2
-
6
x...
Đọc tiếp
Tập nghiệm của hệ bất phương trình x 2 - 4 x + 3 > 0 x 2 - 6 x + 8 > 0 là:
A. (- ∞ ;1) ∪ (4;+ ∞ )
B. (- ∞ ;1) ∪ (3;+ ∞ )
C. (- ∞ ;2) ∪ (3;+ ∞ )
D. (1;4)
Đáp án: A
Ta có bảng xét dấu:

Dựa vào bảng xét dấu ta thấy tập nghiệm của bất phương trình là: (- ∞ ;1) ∪ (4;+ ∞ )
Đúng 0
Bình luận (0)
Hệ bất phương trình
x
2
-
4
x
+
3
0
x
2
-
6...
Đọc tiếp
Hệ bất phương trình x 2 - 4 x + 3 > 0 x 2 - 6 x + 8 > 0 có tập nghiệm là
A.( - ∞ ;1) ∪ (3; + ∞ )
B. ( - ∞ ;1) ∪ (4; + ∞ )
C. ( - ∞ ;2) ∪ (3; + ∞ )
D. (1;4)
Đáp án B.
Ta có:
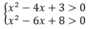
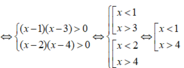
Vậy tập nghiệm của bất phương trình là: ( - ∞ ;1) ∪ (4; + ∞ )
Đúng 0
Bình luận (0)
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình
x
2
+
3
x
x
0
là {0; 3}b) Tập nghiệm của phương trình
x
2
-
4
x
-
2...
Đọc tiếp
Trong các khẳng định sau, số khẳng định đúng là:
a) Tập nghiệm của phương trình x 2 + 3 x x = 0 là {0; 3}
b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0 là {-2}
c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8 là {0}
A. 1
B. 2
C. 0
D. 3
Tập nghiệm của bất phương trình
x
+
1
(
2
x
-
3
)
≥
x
2
+
4
x
-
3
x
+
1
là
Đọc tiếp
Tập nghiệm của bất phương trình x + 1 ( 2 x - 3 ) ≥ x 2 + 4 x - 3 x + 1 là
![]()
![]()
![]()
![]()
Đồ thị hàm số
y
f
(
x
)
x
2
-
4
x
+
3
được cho trong hình 46. Từ hình vẽ nãy hãy chỉ ra tập nghiệm của bất phương trình
x
2
-
4
x
+
3
...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = x 2 - 4 x + 3 được cho trong hình 46. Từ hình vẽ nãy hãy chỉ ra tập nghiệm của bất phương trình x 2 - 4 x + 3 > 0
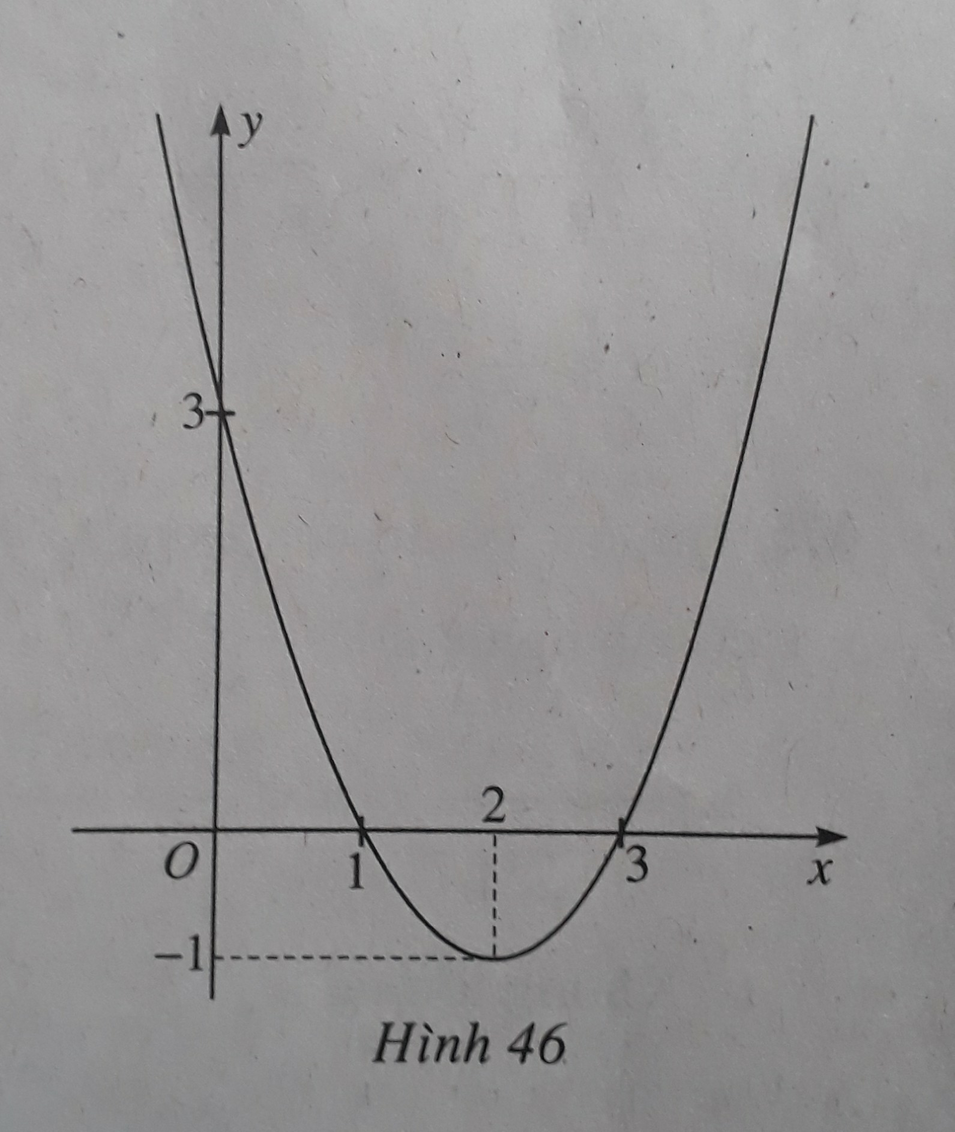
A. x < 1
B. x ≥ 1
C. 1 < x < 3
D. ( - ∞ ; 1 ) ∪ ( 3 ; + ∞ )
Tìm tập nghiệm của bất phương trình l o g 1 5 ( x 2 + 4 x ) ≥ - 1
A. ∅
B. [-5; 1]
C. (-∞; -5] ∪ [1; +∞)
D. [-5; -4) ∪ (0; 1]
Bất phương trình đã cho tương đương với
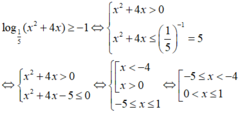
Chọn đáp án D.
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình log 1 2 ( x 2 - 3 x + 3 ) > 0 là
A. (0; 1)
B. (1; 2)
C. (2; 3)
D. (3; 4)
Tập nghiệm của bất phương trình log 1 2 ( x 2 - 3 x + 3 ) > 0 là
A. (0;1)
B. (1;2)
C. (2;3)
D. (3;4)
Tập nghiệm của bất phương trình log 1 2 ( x 2 - 3 x + 3 ) > 0 là
A. (0; 1)
B. (1; 2)
C. (2; 3)
D. (3; 4)