cho 6a - 5b = 1. tìm giá trị nhỏ nhất của 4a2 + 25b2

Những câu hỏi liên quan
cho 6a -5b =1 .tìm giá trị nhỏ nhất của 4a^2+25b^2
Đặt x = 2a; y = -5b.
Áp dụng đẳng thức Bunhiacopski ta có:
\(\left(3x+y\right)^2\le\left(x^2+y^2\right)\left(9+1\right)\Rightarrow x^2+y^2\ge\frac{1}{10}\)
Hay: \(4a^2+25b^2\ge\frac{1}{10}\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{3}{x}=\frac{1}{y}\Leftrightarrow3y=x\Leftrightarrow-15b=2a\Leftrightarrow6a=-45b\)
\(\Leftrightarrow b=-\frac{1}{50};a=\frac{3}{20}\)
Đúng 0
Bình luận (0)
ai giỏi toán giúp mk
6a - 5b = 1
Tìm giá trị nhỏ nhất của 4a^2+25b^2
tích mình trước ik , mình sẽ giải qua tin nhắn cho !
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức .P=/6a-5b/+/7b-4c/+/ab+bc+ca-582/
Giá trị nhỏ nhất của biểu thức B
4
a
2
-
4
a
+
1
+
4
a
2
-
12
a
+
9...
Đọc tiếp
Giá trị nhỏ nhất của biểu thức B = 4 a 2 - 4 a + 1 + 4 a 2 - 12 a + 9
A. 2
B. 1
C. 4
D. 10
Đáp án đúng : A
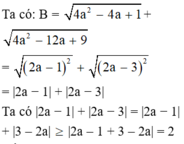
Dấu “=” xảy ra ⇔ 2 a − 1 3 − 2 a ≥ 0 ⇔ 1 2 ≤ a ≤ 3 2
Vậy GTNN của B là 2 khi 1 2 ≤ a ≤ 3 2
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của a và b để biểu thức C=a^2-4ab+5b^2-2b-6 có giá trị nhỏ nhất . Tìm giá trị nhỏ nhất đó.
C=a2-4ab+4b2+b2-2b+1-7=(a-2b)2+(b-1)2-7 > hoặc =-7
dấu = xảy ra khi a-2b=0
b-1=0
<=>a=2;b=1
..................................
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a. y=\(\sqrt{\text{3(1+ sin(x))}}\)-5
b. y= 6 sin(x+8)-5
P = 4a2 + 4ab + 4b2 - 12a -12b + 12 . Giá trị nhỏ nhất của P = bao nhiêu?
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
Đúng 0
Bình luận (0)
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
Đúng 0
Bình luận (0)
Tìm a để giá trị của mỗi phân thức sau được xác định:a)
a
2
−
1
9
a
2
−
16
;
b)
2
a
+
1
a
2...
Đọc tiếp
Tìm a để giá trị của mỗi phân thức sau được xác định:
a) a 2 − 1 9 a 2 − 16 ; b) 2 a + 1 a 2 − 6 a + 9 ;
c) 3 a − 4 2 a 2 + 3 a ; d) a + 1 a 3 − 4 a 2 + 3 a .
a) a ≠ ± 4 3 b) a ≠ 3
c) a ≠ 0, a ≠ - 3 2 d) a ≠ 0, a ≠ 1, a ≠ 3
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sau:
A= x2-3x+5
B= (2x-1)2+(x+2)2
a) Ta có: \(A=x^2-3x+5\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{11}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
b: Ta có: \(B=\left(2x-1\right)^2+\left(x+2\right)^2\)
\(=4x^2-4x+1+x^2+4x+4\)
\(=5x^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x=0
Đúng 0
Bình luận (0)
















