Cho tứ giác ABCD.Chứng minh nếu AD+AC < BD+BC thì AD < BD

Những câu hỏi liên quan
Cho tứ giác ABCD
Chứng minh:
a) Tổng 2 cạnh đối nhỏ hơn tổng 2 đường chéo
b) Nếu AD + AC bé hơn BD +BC thì AD bé hơn BD
Cho tứ giác ABCD. Chứng minh rằng nếu |vecto AD + vecto BC| = |vecto AB + vecto DC| thì AC vuông góc với BD
Cho hình thang ABCD có AB // CD. Chứng minh rằng: Nếu AD+AC=BC+BD thì tứ giác ABCD là hình thang cân
Cho tứ giác ABCD.Cmr:
AD+AC<BD+BC thì AD<BD
cho tứ giác ABCD. Chứng minh rằng:
a) Nếu AC=AD thì BC<BD
b)Nếu chu vi tam giác ADB không lớn hơn chu vi tam giác ACD thì AB<AC
cho tứ giác ABCD Chứng minh rằng :
a) Nếu AC=AD thì BC<BD
b) Nếu chu vi tam giác ABD không lớn hơn chu vi tam giác ACD thì AB<AC
Cho hình thang ABCD (AB//CD). Chứng minh rằng nếu AD+AC=BC+BD thì tứ giác ABCD là hình thang cân. Giúp mình gấp với.
Chứng minh rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ BD thì AD ⊥ BC.
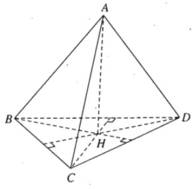
Vẽ AH ⊥ (BCD) tại H, ta có CD ⊥ AH và vì CD ⊥ AB ta suy ra CD ⊥ BH. Tương tự vì BD ⊥ AC ta suy ra BD ⊥ CH
Vậy H là trực tâm của tam giác BCD tức là DH ⊥ BC
Vì AH ⊥ BC nên ta suy ra BC ⊥ AD
Cách khác: Trước hết ta hãy chứng minh hệ thức:
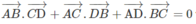
với bốn điểm A, B, C, D bất kì.
Thực vậy , ta có:
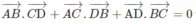
Do đó nếu AB ⊥ CD nghĩa là
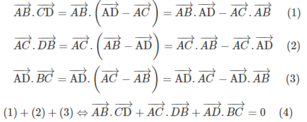
Từ hệ thức (4) ta suy ra
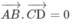 ,
,
do đó AD ⊥ BC.
Đúng 0
Bình luận (0)
Cho tứ giác ABCD.Chứng minh rằng : AB+BC+CD+DA / 2 < AC+BD < AB+BC+CD+DA.
Áp dụng bđt trong tam giác , ta có :
AB < OB + OA ; BC < OB + OC ; CD < OC + OD ; AD < OA + OD
=> AB +BC + CD + AD < 2(OA + OB + OC + OD)
=> (AB+BC+CD+AD)/2<AC+BD (1)
AB + BC > AC ; BC + CD > BD ; CD + AD > AC ; AB + AD > BD=> 2(AB + BC + CD + DA) > 2(AC + BD)
=> AB + BC + CD + DA > AC + BD (2)
Từ (1) và (2) suy ra đpcm
Đúng 2
Bình luận (0)












