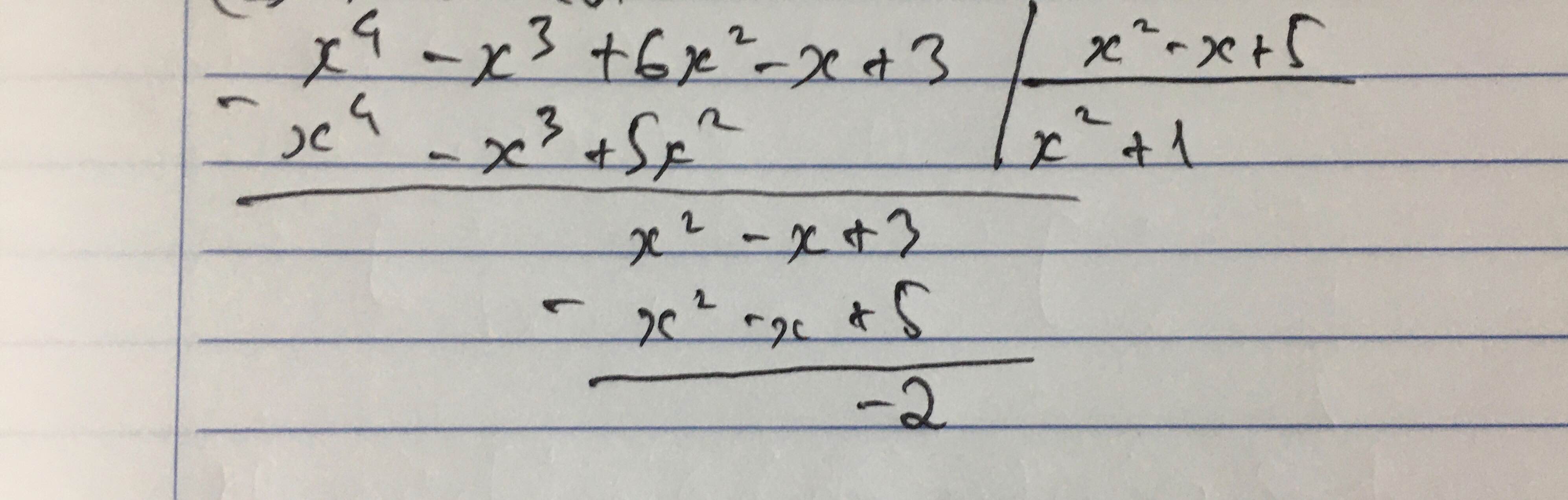cho đa thức p(x)=x2+bx+c biết q(x)=x4+6x2+25; r(x)=3x4+4x2+28x+5 đều chia hết cho p(x).. chứng tỏ 2020 chia hết cho p(-3)

Những câu hỏi liên quan
Cho đa thức P(x) = x2+bx+c, trong đó b và c là các số nguyên.Biết rằng đa thức x4 + 6x2+25 và 3x4+4x2+28x+5 đều chia hết cho P(x).
Cho đa thức P(x) = x2+bx+c, trong đó b và c là các số nguyên.Biết rằng đa thức x4 + 6x2+25 và 3x4+4x2+28x+5 đều chia hết cho P(x).
Cho đa thức P(x) = x2+bx+c, trong đó b và c là các số nguyên.Biết rằng đa thức x4 + 6x2+25 và 3x4+4x2+28x+5 đều chia hết cho P(x).
Tính P(1)
Theo đề bài, ta có:
Vì \(x^4+6x^2+25\) chia hết cho \(P\left(x\right)\) \(\Rightarrow\) \(3\left(x^4+6x^2+25\right)\) chia hết cho \(P\left(x\right)\)
và \(3x^4+4x^2+28x+5\) chia hết cho \(P\left(x\right)\)
nên \(\left[3\left(x^4+6x^2+25\right)-\left(3x^4+4x^2+28x+5\right)\right]\) chia hết cho \(P\left(x\right)\)
\(\Leftrightarrow\) \(\left(3x^4+18x^2+75-3x^4-4x^2-28x-5\right)\) chia hết cho \(P\left(x\right)\)
\(\Leftrightarrow\) \(14x^2-28x+70\) chia hết cho \(P\left(x\right)\)
\(\Leftrightarrow\) \(x^4-2x+5\) chia hết cho \(P\left(x\right)\), tức \(x^4-2x+5\) chia hết cho \(x^2+bx+c\) \(\left(\text{*}\right)\)
Mà \(b;\) \(c\) là các số nguyên nên từ \(\left(\text{*}\right)\), suy ra \(b=-2;\) \(c=5\)
Khi đó, \(P\left(1\right)=1^2-2.1+5=4\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chia đa thức cho đa thức: (mình cần gấppppppp
(x4-x3+6x2-x+3) : (x2-x+5)
Ta có: \(\dfrac{x^4-x^3+6x^2-x+3}{x^2-x+5}\)
\(=\dfrac{x^4-x^3+5x^2+x^2-x+5-2}{x^2-x+5}\)
\(=x^2+1-\dfrac{2}{x^2-x+5}\)
Đúng 0
Bình luận (0)
Tìm a để đa thức x 4 - x 3 + 6 x 2 - x + a chia hết cho đa thức x 2 - x + 5
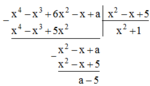
Để có phép chia hết thì số dư phải bằng 0.
Ta có: a – 5 = 0 hay a = 5.
Đúng 0
Bình luận (0)
Tìm n để đa thức x4 -x3+6x2-x+n chia hết cho đa thức x2-x+5
Để \(x^4-x^3+6x^2-x+n⋮x^2-x+5\) thì
\(n-5=0\Rightarrow n=5\)
Vậy để \(x^4-x^3+6x^2-x+n⋮x^2-x+5\) thì \(n=5\)
Đúng 2
Bình luận (0)
Phân tích đa thức thành nhân tử:
a.10x2y – 20xy2 b. x2 – y2 + 10y – 25 c. x2 – y2 + 3x – 3y
d. x3 + 3x2 – 16x – 48 e. 9x3 + 6x2 + x f. x4 + 5x3 + 15x – 9
\(a,10x^2y-20xy^2=10xy\left(x-2y\right)\\ b,x^2-y^2+10y-25=x^2-\left(y^2-10y+25\right)=x^2-\left(y-5\right)^2=\left(x-y+5\right)\left(x+y-5\right)\\ c,x^2-y^2+3x-3y=\left(x-y\right)\left(x+y\right)+3\left(x-y\right)=\left(x-y\right)\left(x+y+3\right)\\ d,x^3+3x^2-16x-48=\left(x^3+3x^2\right)-\left(16x+48\right)=x^2\left(x+3\right)-16\left(x+3\right)=\left(x+3\right)\left(x^2-16\right)=\left(x+3\right)\left(x+4\right)\left(x-4\right)\)
\(e,9x^3+6x^2+x=x\left(9x^2+6x+1\right)=x\left(3x+1\right)^2\\ f,x^4+5x^3+15x-9=\left(x^4+5x^3-3x^2\right)+\left(3x^2+15x-9\right)=x^2\left(x^2+5x-3\right)+3\left(x^2+5x-3\right)=\left(x^2+3\right)\left(x^2+5x-3\right)\)
Đúng 0
Bình luận (0)
Tìm a và b để đa thức A chia hết cho đa thức B với:a) A
x
4
-
x
3
+
6
x
2
- x + a và B
x
2
- x + 5;b) A
x
4
-
9
x
3
+ 21
x
2
+...
Đọc tiếp
Tìm a và b để đa thức A chia hết cho đa thức B với:
a) A = x 4 - x 3 + 6 x 2 - x + a và B = x 2 - x + 5;
b) A = x 4 - 9 x 3 + 21 x 2 +ax + b và B = x 2 - x - 2.

Hay a − 1 = 0 b + 30 = 0 ⇒ a = 1 b = − 30 .
Đúng 0
Bình luận (0)
Đa thức x4−x3+6x2−x+a chia hết cho đa thức x2−x+5 Khi : a. a= -7 b. a = 7 c. a = - 5 d. a = 5
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]f(x)ax4+bx3+cx2+dx+ef(x)ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.Cm đa thức không có nghiệm hữu tỉ2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZCmR các hệ số của P(x) chia hết cho 7.3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)10; P(2)20; P(3)30.Tính P(12)+P(−8)10P(12)+P(−8)104. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)5. Tìm đa thức bậc 3 có hệ số cao...
Đọc tiếp
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]
f(x)=ax4+bx3+cx2+dx+ef(x)=ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.
Cm đa thức không có nghiệm hữu tỉ
2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZ
CmR các hệ số của P(x) chia hết cho 7.
3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)=10; P(2)=20; P(3)=30.
Tính P(12)+P(−8)10P(12)+P(−8)10
4. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)
5. Tìm đa thức bậc 3 có hệ số cao nhất là 1 sao cho P(1)=1; P(2)=2; P(3)=3
6. Cho đa thức P(x) có bậc 6 có P(x)=P(-1); P(2)=P(-2); P(3)=P(-3). CmR: P(x)=P(-x) với mọi x
7. Cho đa thức P(x)=−x5+x2+1P(x)=−x5+x2+1 có 5 nghiệm. Đặt Q(x)=x2−2.Q(x)=x2−2.
Tính A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5)A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5) (x1,x2,x3,x4,x5x1,x2,x3,x4,x5 là các nghiệm của P(x))