các phần tử của x để cănx + căn-x có nghĩa
Cho Các biểu thức
A=căn x+2 × căn x-3 và B = căn (x+2)×(x-3)
a) Tìm x để A có nghĩa.Tìm x để B có nghĩa
b) Với giá trị nào của x thì A=B
Các bn giúp mk giải rõ ràng ra nhé...Thanks trước
a/
\(A=\sqrt{x+2}.\sqrt{x-3}\)
ĐKXĐ: \(\hept{\begin{cases}x+2\ge0\\x-3\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ge-2\\x\ge3\end{cases}\Rightarrow}x\ge3}\)
\(B=\sqrt{\left(x+2\right)\left(x-3\right)}\)
ĐKXĐ: \(\hept{\begin{cases}x+2\ge0\\x-3\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ge-2\\x\ge3\end{cases}\Rightarrow}x\ge3}\)
b/ A = B \(\Leftrightarrow\sqrt{x+2}.\sqrt{x-3}=\sqrt{\left(x+2\right)\left(x-3\right)}\)
\(\Rightarrow\sqrt{\left(x+2\right)\left(x-3\right)}=\sqrt{\left(x+2\right)\left(x-3\right)}\) (đúng)
Vậy với mọi giá trị của \(x\in R\) thì A = B
Cho đa giác đều 32 cạnh. Gọi S là tập hợp các tứ giác tạo thành có 4 đỉnh lấy từ các đỉnh của đa giác đều. Chọn ngẫu nhiên một phần tử của S. Xác suất để chọn được một hình chữ nhật là
A. 1 341
B. 1 385
C. 1 261
D. 1 899
Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2
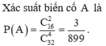
Chọn D
cho tập hợp A = [ x / x E N* , x < 199 ]
a, tập hợp A có mấy tập hợp con
b,tính tổng cac phần tử của A
c,nếu viết liên tiếp các phần tử của A ta được một số 1,2,3,4,5,6,7,8,9,10.11.12,............198,199.Tính tổng các chữ số của số đó.
Mong các bạn giúp với mai nộp rồi
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số ![]() có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
A. 1
B. 0
C. 2
D. 4
Cho đa giác đều 32 cạnh. Gọi S là tập hợp cáctứ giác tạo thành có 4 đỉnh lấy từ các đỉnh của đa giác đều. Chọn ngẫu nhiên một phần tử của S . Xác suất để chọn được một hình chữ nhật là
A. 1 341 .
B. 1 385 .
C. 1 261 .
D. 3 899 .
Đáp án D
Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2 .
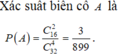
Tìm x để các căn thức sau có nghĩa:
a)\(\sqrt{2X^2+6}\)
Đẳng thức có nghĩa \(\Leftrightarrow2x^2+6\ge0\)
Mà: \(x^2\ge0\forall x\)
\(\Rightarrow2x^2\ge0\forall x\)
\(\Rightarrow2x^2+6>0\forall x\)
Vậy đẳng thức luôn có nghĩa
vì 2x^2 luôn lớn hơn 0 suy ra x k cần đk để căn thức có nghĩa
AI BIẾT LÀM BÀI NÀY CHỈ EM VỚI Ạ!! THANK YOU✿
Cho tập hợp A = { a,b,c,d }
a) Viết các tập hợp con của A có 1 phần tử, có 2 phần tử, có 3 phần tử.
b) Tập hợp A có bao nhiêu tập hợp con?
a, {a}; {b}; {c} ; {d}
{a;b}; {a;c}; {a;d}; {b;c}; {b;d}; {c;d}
{a;b;c}; {a;b;d}; {a;c;d}; {b;c;d}
b, Số tập con: 24= 16(tập con)
cho M = {a;b;c}
a) viết các tập hợp con của M mà mổi tập hợp có hai phần tử
b)dùng kí hiệu < để thể hiện quan hệ giửa các tập hợp con đó với tập hợp M
a, A = { a; b }
B = { a; c }
C = { b; c }
b, A < M
B < M
C < M
a) A = a;b
B = a;c
C = b;c
b) A < M
B < M
C < M
Theo mk nghĩ là z
Tk mk nha!!!
Tìm x để các căn thức sau có nghĩa:
a) \(\sqrt{2x^{2\:\:}+6}\)
Đẳng thức có nghĩa \(2x^2+6\ge0\)
Ma \(^{x^2\ge0\forall x}\)
=>\(2x^2\ge0\forall x\)
=>\(2x^2+6\ge0\forall x\)
Vậy đẳng thức thì luôn có nghĩa