Cho góc xOy và một điểm M nằm trong góc đó. Hãy dựng qua O một đường thẳng cắt Ox ở A, cắt Oy ở B sao cho M là trung điểm của AB.

Những câu hỏi liên quan
Cho góc xOy và một điểm M nằm trong góc đó. Hãy dựng qua O một đường thẳng cắt Ox ở A, cắt Oy ở B sao cho M là trung điểm của AB.
Cho điểm M nằm trong góc xOy. Hãy dựng một đường thẳng (d) đi qua M, cắt Ox, Oy lần
lượt tại A, B sao cho M là trung điểm AB.
Cho góc xOy và điểm A nằm trong góc đó. Từ đó suy ra cách dựng hình đường thẳng đi qua A, cắt OX, Oy ở C, D sao cho A là trung điểm của CD.
Cách dựng:
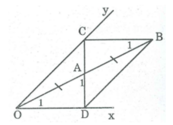
- Dựng B đối xứng với O qua A.
- Qua B dựng đường thẳng song song Ox cắt Oy tại C.
- Dựng tia CA cắt Ox tại D.
Ta có D là điểm cần dựng.
Chứng minh:
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.
Đúng 0
Bình luận (0)
Cho góc xOy và điểm A nằm trong góc đó
a) Vẽ điểm B đối xứng với O qua A. Qua B kẻ đường thẳng song song với Ox, cắt Oy ở C. Gọi D là giao điểm của CA và Ox. Chứng minh rằng các điểm C và D đối xứng với nhau qua điểm A
b) Từ đó suy ra cách dựng đường thẳng đi qua A, cắt Ox, Oy ở D, C sao cho A là trung điểm của CD
Cho góc xOy nhỏ hơn 180 và một điểm M nằm trong góc đó. Qua M hãy dựng đường thẳng cắt các tia Ox, Oy tại A,B sao cho diện tích tam giác OAB nhỏ nhất?
Cho góc xOy khác góc bẹt và điểm M nằm trong góc ấy.
a) Qua M dựng đường thẳng cắt các tia Ox, Oy theo thứ tự ở A và B sao cho M là trung điểm AB
b) CM rằng tg AOB nhận được trong cách dựng trên có diện tích luôn nhỏ nhất trong các tam giác tạo bởi các tia Ox, Oy và 1 đường bất kì đi qua M.
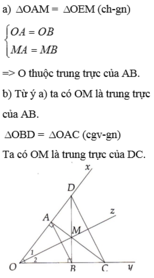
Cho góc xOy khác góc bẹt Oz là tia phân giác của góc xOy. Gọi M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:a) Điểm O thuộc đường trung trực của AB;b) OM là đường trung trực của AB; Điểm M thuộc đường trung trực của CD.
Đọc tiếp
Cho góc xOy khác góc bẹt Oz là tia phân giác của góc xOy. Gọi M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:
a) Điểm O thuộc đường trung trực của AB;
b) OM là đường trung trực của AB; Điểm M thuộc đường trung trực của CD.
Cho góc vuông xOy. Lấy các điểm I và K lần lượt trên các tia Ox và Oy. Đường tròn (I; OK) cắt tia Ox tại M (I nằm giữa O và M), đường tròn (K; OI) cắt tia Oy tại N (K nằm giữa O và N)a, Chứng minh (I) và (K) luôn cắt nhaub, Tiếp tuyến tại M của (I), tiếp tuyến tại N của đường tròn (K) cắt nhau tại C. Chứng minh tứ giác OMCN là hình vuôngc, Gọi A, B là các giao điểm của (I) và (K) trong đó B ở miền trong góc xOy. Chứng minh ba điểm A, B, C thẳng hàngd, Giả sử I và K thứ tự di động trên các tia Ox...
Đọc tiếp
Cho góc vuông xOy. Lấy các điểm I và K lần lượt trên các tia Ox và Oy. Đường tròn (I; OK) cắt tia Ox tại M (I nằm giữa O và M), đường tròn (K; OI) cắt tia Oy tại N (K nằm giữa O và N)
a, Chứng minh (I) và (K) luôn cắt nhau
b, Tiếp tuyến tại M của (I), tiếp tuyến tại N của đường tròn (K) cắt nhau tại C. Chứng minh tứ giác OMCN là hình vuông
c, Gọi A, B là các giao điểm của (I) và (K) trong đó B ở miền trong góc xOy. Chứng minh ba điểm A, B, C thẳng hàng
d, Giả sử I và K thứ tự di động trên các tia Ox và Oy sao cho OI + OK = a không đổi. Chứng minh đường thẳng AB luôn đi qua một điểm cố định

a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C
Đúng 0
Bình luận (0)
Bài 1: Cho góc nhọn xOy. Lấy điểm A thuộc tia Ox, lấy B thuộc tia Oy sao cho OA OB. Qua A kẻ đường thẳng vuông góc với tia Ox cắt tia Oy tại M, qua B kẻ đường thẳng vuông góc với tia Oy cắt tia Ox tại N. Gọi H là giao điểm của AM và BN, I là trung điểm của MN. CMRa, ONOM và AN-BMb, Tia OH là tia phân giác của góc xOyc, Ba điểm O, H, I thẳng hàngBài 2:Cho tam giác ABC, M là trung điểm của AB. Đường thẳng qua M và song song vs BC cắt AC ở I, đường thẳng qua I và song song với AB cắt BC ở K. CMR:a...
Đọc tiếp
Bài 1:
Cho góc nhọn xOy. Lấy điểm A thuộc tia Ox, lấy B thuộc tia Oy sao cho OA = OB. Qua A kẻ đường thẳng vuông góc với tia Ox cắt tia Oy tại M, qua B kẻ đường thẳng vuông góc với tia Oy cắt tia Ox tại N. Gọi H là giao điểm của AM và BN, I là trung điểm của MN. CMR
a, ON=OM và AN-BM
b, Tia OH là tia phân giác của góc xOy
c, Ba điểm O, H, I thẳng hàng
Bài 2:
Cho tam giác ABC, M là trung điểm của AB. Đường thẳng qua M và song song vs BC cắt AC ở I, đường thẳng qua I và song song với AB cắt BC ở K. CMR:
a, AM=IK
b, AMI=IKC
c, AI=IC