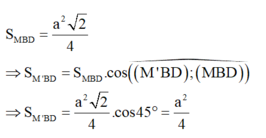cho hình vuông abcd có cạnh bằng a có tâm o gọi m,n trung điểm ao,cd cm tam giá bmn vuông cân

Những câu hỏi liên quan
cho hình vuông ABCD tâm o cạnh bằng a . gọi M,N là trung điểm của CD và AO .
1)chứng minh BCMN nội tiếp
2) tính diện tích tam giác BMN theo a
Cho hình lập phương ABCD. ABCD có cạnh bằng a. Gọi O và O lần lượt là tâm các hình vuông ABCD và ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Tính thể tích khối tứ diện OOMN. A.
a
3
8
B. a3 C.
a
3
12
D.
a
3
24
Đọc tiếp
Cho hình lập phương ABCD. A'B'C'D' có cạnh bằng a. Gọi O và O' lần lượt là tâm các hình vuông ABCD và A'B'C'D'. Gọi M, N lần lượt là trung điểm của các cạnh B'C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a3
C. a 3 12
D. a 3 24
Chọn D
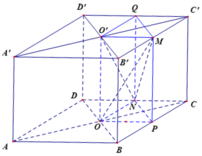
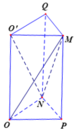
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có S ∆ O P N = 1 4 S ∆ B C D = 1 8 S A B C D = a 2 8 ⇒ V O P N . O ' M Q = a 3 8
mà
V O O ' M N = V O P N . O ' M Q - V M . O P N - V N . O ' M Q = a 3 8 - 1 3 . a 3 8 - 1 3 . a 3 8 = a 3 24
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. M, N, P lần lượt là trung điểm của AO, OB, CD.
a,Chứng minh: AMNB là hình thang cân
b, Chứng minh MNPD là hình bình hành
c, Chứng minh: DM vuông góc AN
d, Gọi I là trung điểm của AP
CM tam giác DIN cân
MN là đường trung bình của tam giác AOB
\(\Rightarrow MN\)//AB
AM=NB=\(\frac{1}{2}OA\)=\(\frac{1}{2}OB\)
\(\Rightarrow AMNB\)là hình thang cân
MN//AB\(\Rightarrow MN\)//OB (1)
MN=\(\frac{1}{2}AB=\frac{1}{2}DC=DP\) (2)
từ (1),(2) suy raMNPD là hình bình hành
Xét tap giác DMB
MO vừa là đường tuy tuyến vừa là đường cao
suy ra DMB là tam giác cân
suy ra MBD=MDB (1)
tam giác OAN=tam giác OBM(tự chứng minh)
suy ra MBO=OAN(2)
từ 1 và 2 suy ra
OAN=MDB
mà DNP=MDB(SLT)
su ra DNP=OAN
xét tam giác OAN
OAN+ONA=90 độ
suy ra DNP + ONA=90 độ
suy ra NP vuông góc AN
mà DM//NP
suy ra DM vuông góc AN
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD có AB = a , BC=b , K là chân đường vuông góc hạ từ B tới đoạn AC , gọi M, N lần lượt là trung điểm của AK và CD ; tìm điều kiện của a,b để tam giác BMN vuông cân tại M
2/Cho h ình thoi có độ dài hai đường chéo bằng 6cm và 8cm .Tính độ dài cạnh hình thoi?3/Cho hình thang ABCD có AB // CD, AB 4, CD 12.Tính độ dài đường TB của hình thang4/Tam giác ABC vuông tại A, BC 7cm, MB MC, M BC.Tính độ dài AM?5/Cho tam giác ABC có M,N theo thứ tự là trung điểm của AB và AC.Biết MN 4,5 cm.Tính độ dài cạnh BC.6/Cho hình thang ABCD (AB//CD),gọi E,F theo thứ tự là trung điểm của AD và BC.Biết EF 6cm, AB 4cm ,tính độ dài cạnh CD?7/Hình thang có độ dài đáy lớn gấp đôi đáy...
Đọc tiếp
2/Cho h ình thoi có độ dài hai đường chéo bằng 6cm và 8cm .Tính độ dài cạnh hình thoi?
3/Cho hình thang ABCD có AB // CD, AB = 4, CD = 12.Tính độ dài đường TB của hình thang
4/Tam giác ABC vuông tại A, BC = 7cm, MB = MC, M BC.Tính độ dài AM?
5/Cho tam giác ABC có M,N theo thứ tự là trung điểm của AB và AC.Biết MN = 4,5 cm.Tính độ dài cạnh BC.
6/Cho hình thang ABCD (AB//CD),gọi E,F theo thứ tự là trung điểm của AD và BC.Biết EF = 6cm, AB = 4cm ,tính độ dài cạnh CD?
7/Hình thang có độ dài đáy lớn gấp đôi đáy nhỏ . Độ dài đường trung bình là 12 cm. Tính độ dài 2 đáy.
8/Cho hình chữ nhật ABCD, hai đường chéo AC và BD cắt nhau tại O, biết AO = 3cm, Tính độ dài BD?
9/Cho ABC và một điểm O tuỳ ý . Vẽ A/B/C/ đối xứng với ABC qua điểm O .
10/Cho hình vuông ABCD có độ dài đường chéo bằng 10cm.Tính cạnh hình vuông?
11/Cho hình vuông ABCD có độ dài cạnh bằng 3.Tính độ dài đường chéo của hình vuông?
12/T ính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các
cạnh góc vuông bằng 3 cm v à 4 cm.
có làm thì mới có ăn
Cho hình vuông ABCD có độ dài cạnh bằng a. Gọi M và N lần lượt là trung điểm của AB và AC . Các đường thẳng DN và CM cắt nhau tại I . CHứng minh rằng :
a, Tam giác CIN vuông tại I ( mình làm được rồi)
b, Tam giác AID cân tại A ( mình làm được rồi)
c, Gọi O là tâm đối xứng của hình vuông ABCD . Tính góc DIO? ( mình chưa làm được)
đề bài sai rồi bn mk vẽ hình cho bn xem nè
M, N là td cùa AB,AC nhưng tam giác CIN ko vuông
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD trên đoạn AC lấy M sao cho AC=4AM và N là trung điểm cạnh CD
CMR: Tam giác BMN là tam giác vuông cân
Bài 1. Cho hình vuông ABCD có cạnh bằng a. Trên cạnh BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. a) Chứng minh tam giác AMN là tam giác vuông cân. b) Gọi E là trung điểm của MN. Tia AE cắt CD tại F. Chứng minh tam giác FAN = tam giác FAM.
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)
Đúng 3
Bình luận (0)
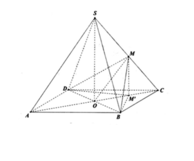
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M BD bằng: A.
a
2
6
8
B.
a
2
2
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của ABCD. Gọi M là trung điểm SC và M' là hình chiếu vuông góc của M lên (ABCD). Diện tích của tam giác M' BD bằng:
A. a 2 6 8
B. a 2 2
C. 2 a 2 8
D. a 2 4