Từ ba đỉnh A, B, C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt BC và các đường thẳng CA, BA tại D, E, F.
Chứng minh rằng:
a) 1/AD = 1/BE + 1/CF
b) Diện tích SΔDEF = 2SΔABC

Những câu hỏi liên quan
Từ ba đỉnh A, B, C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt BC và các đường thẳng CA, BA tại D, E, F.
Chứng minh rằng:
a) 1/AD = 1/BE + 1/CF
b) Diện tích SΔDEF = 2SΔABC
Từ ba đỉnh A, B, C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt BC và các đường thẳng CA, BA tại D, E, F.
Chứng minh rằng:
a) 1/AD = 1/BE + 1/CF
b) Diện tích SΔDEF = 2SΔABC
Từ ba đỉnh A, B, C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt BC và các đường thẳng CA, BA tại D, E, F.
Chứng minh rằng:
a) 1/AD = 1/BE + 1/CF
b) Diện tích SΔDEF = 2SΔABC
Cần giúp câu b.
Từ ba đỉnh A, B, C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt BC và các đường thẳng CA, BA tại D, E, F.
Chứng minh rằng:
a) 1/AD = 1/BE + 1/CF
b) Diện tích SΔDEF = 2SΔABC
Help me !!!!
từ 3 đỉnh A,B,C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt cạnh BC và các đường thẳng CA, AB tại D,E,F chứng minh rằng:
a. 1/AD=1/BE+1/CF
b. S DEF =2S ABC
Lưu ý S là diện tích nha
Từ ba đỉnh A, B, C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt BC và các đường thẳng CA, BA tại D, E, F.
Chứng minh rằng:
a) 1/AD = 1/BE + 1/CF
b) Diện tích SΔDEF = 2SΔABC
Từ ba đỉnh A, B, C của tam giác ABC vẽ ba đường thẳng song song với nhau, chúng lần lượt cắt BC và các đường thẳng CA, BA tại D, E, F.
Chứng minh rằng:
a) 1/AD = 1/BE + 1/CF
b) Diện tích SΔDEF = 2SΔABC
Em chỉ cần làm câu b thôi ạ :) mong mọi người giúp đỡ...help
a) Áp dụng hệ quả định lý \(Ta-lét\) vào \(\Delta BEC\) có \(AD//BE\left(gt\right)\) \(\Rightarrow\dfrac{AD}{BE}=\dfrac{CD}{BC}\left(2\right)\)
Áp dụng hệ quả định lý \(Ta-lét\) vào \(\Delta BFC\) có \(AD//CF\left(gt\right)\) \(\Rightarrow\dfrac{AD}{CF}=\dfrac{BD}{BC}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\dfrac{AD}{BE}+\dfrac{AD}{CF}=\dfrac{CD}{BC}+\dfrac{BD}{BC}\)
\(\Rightarrow AD\left(\dfrac{1}{BE}+\dfrac{1}{CF}\right)=\dfrac{CD+BD}{BC}=\dfrac{BC}{BC}=1\\ \Rightarrow\dfrac{1}{BE}+\dfrac{1}{CF}=\dfrac{1}{AD}\left(đpcm\right)\)
b) Áp dụng hệ quả định lý \(Ta-lét\) vào \(\Delta BAE\) có \(BE//CF\left(gt\right)\) \(\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{\: AB}\)
Xét \(\Delta EAF\) và \(\Delta CAB\) có: \(\left\{{}\begin{matrix}\dfrac{AE}{AC}=\dfrac{AF}{\: AB}\left(\text{Chứng minh trên}\right)\\\widehat{EAF}=\widehat{CAB}\left(\text{2 góc đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta EAF\sim\Delta CAB\left(c.g.c\right)\\ \Rightarrow\widehat{AEF}=\widehat{ACB}\left(\text{2 góc tương ứng}\right)\\ \Rightarrow EF//BC\left(\text{2 góc so le trong}\right)\)
Mà \(BE//CF\left(gt\right)\)
\(\Rightarrow\text{Tứ giác }BECF\text{ là hình bình hành}\left(\text{Dấu hiệu nhận biết}\right)\\ \Rightarrow A\text{ là trung điểm }EC\left(\text{Tính chất đường chéo hình bình hành}\right)\\ \Rightarrow AC=\dfrac{1}{2}AE\\ \Rightarrow S_{ABC}=\dfrac{1}{2}S_{BEC}\left(\text{Chung đường cao hạ từ B xuống EC}\right)\left(5\right)\)
Từ \(E\) kẻ \(EI\perp BC\Rightarrow EI\) là đường cao ứng với \(BC\) của \(\Delta EBC\)
Từ \(D\) kẻ \(DK\perp EF\Rightarrow DK\) là đường cao ứng với \(EF\) của \(\Delta EDF\)
Ta có : \(DI//EK\left(I\in BC;K\in EF;BC//EF\right)\left(3\right)\)
\(\Rightarrow EI\perp EK\left(EI\perp DI\right)\\ \Rightarrow EI//DK\left(\text{Cùng }\perp EK\right)\left(4\right)\)
Từ \(\left(3\right)\) và \(\left(4\right)\Rightarrow\text{Tứ giác }DIEK\text{ là hình bình hành}\left(\text{Dấu hiệu nhận biết}\right)\)\(\Rightarrow DI=EK\left(\text{2 cạnh đối hình bình hành}\right)\)
Mà \(EF=BC\left(\text{2 cạnh đối hình bình hành}\right)\)
\(\Rightarrow S_{DEF}=S_{EBC}\left(6\right)\)
Từ \(\left(5\right)\) và \(\left(6\right)\Rightarrow S_{ABC}=\dfrac{1}{2}S_{DEF}\)
\(\Rightarrow S_{DEF}=2S_{ABC}\left(đpcm\right)\)
Đúng 0
Bình luận (2)
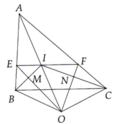
Cho tam giác ABC, đường phân giác của góc B và đường phân giác của C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E, F.a) Chứng mình BEI, CFI là các tam giác cân.b) Chứng minh BE + CF EF.c) Gọi M là trung điểm của IB, N là trung điểm của IC, các đường thẳng EM, FN cắt nhau tại O. Chứng minh OB OC.d) Chứng minh ba điểm A, I, O thẳng hàng.
Đọc tiếp
Cho tam giác ABC, đường phân giác của góc B và đường phân giác của C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E, F.
a) Chứng mình BEI, CFI là các tam giác cân.
b) Chứng minh BE + CF = EF.
c) Gọi M là trung điểm của IB, N là trung điểm của IC, các đường thẳng EM, FN cắt nhau tại O. Chứng minh OB = OC.
d) Chứng minh ba điểm A, I, O thẳng hàng.
Cho tam giác ABC vuông tại A, có đường cao AH ( AB AC ). Vẽ đường tròn (B;BA) cắt đường thẳng AH tại D) (D khác A).a) Chứng minh H là trung điểm của AD và tam giác CAD cân.b) Chứng minh CD là tiếp tuyến của đường tròn (B; BA).c) Vẽ đường kính AK của đường tròn (B;BA). Từ K vẽ đường thẳng vuông góc với AK cắtđường thẳng AD tại N. Chứng minh DN.DC DB.DKd) Từ điểm M thuộc cung nhỏ AD của đường tròn (B;BA) vẽ tiếp tuyến cắt AC và CD lầnlượt tại E và F. Chứng minh rằng: Nếu diện tích tứ giác ABDC g...
Đọc tiếp
Cho tam giác ABC vuông tại A, có đường cao AH ( AB < AC ). Vẽ đường tròn (B;
BA) cắt đường thẳng AH tại D) (D khác A).
a) Chứng minh H là trung điểm của AD và tam giác CAD cân.
b) Chứng minh CD là tiếp tuyến của đường tròn (B; BA).
c) Vẽ đường kính AK của đường tròn (B;BA). Từ K vẽ đường thẳng vuông góc với AK cắt
đường thẳng AD tại N. Chứng minh DN.DC = DB.DK
d) Từ điểm M thuộc cung nhỏ AD của đường tròn (B;BA) vẽ tiếp tuyến cắt AC và CD lần
lượt tại E và F. Chứng minh rằng: Nếu diện tích tứ giác ABDC gấp 4 lần diện tích tam giác EBF
thì CE +CF = 3EF .