cho tam giác MNP cân tại M có MD là dường phân giác
a) chứng minh tam giacs MND= tam giác MPD
b) gọi G là trọng tâm của tam giác MNP chứng minh 3 diểm MGD thẳng hàng
c) biết cạnh MN =13 cm cạnh NP = 9 cm tính đọ dài của đoạn GD và GM

Những câu hỏi liên quan
cho tam giác MNP cân tại M . Biết MN=10 cm,ND = 12cm.Kẻ phân giác MD của góc NMP(D thuộc NP)
a) CM: tam gác MND=MPD
b) CM: Tam giác MND vuông.Tính MD
c)Qua D kẻ đoạn thẳng song song MP cắt MN tại I. Gọi H là trọng tâm của tam giác MNP
CM I,G,P thẳng hảng
a. xét tg MND và tg MPD có : MD chung
^PMD = ^NMD do MD là pg của ^PMN (Gt)
MN = MP do tg MNP cân tại M (gt)
=> tg MND = tg MPD (c-g-c)
b. tg MNP cân tại A (gt) có MD là pg
=> MD đồng thời là đường cao (đl) và là trung tuyến => DN = 6
=> tg MND vuông tại D (Đn)
=> MN^2 = MD^2 + DN^2 (đl Pytago)
DN = 6; MN =10
=> MD = 8 do MD > 0
c.
cho tam giac MNP vuông tại M( MN>MP). trên cạnh NP lấy điểm E sao cho NE = NM, qua E kẻ đừơng thăng vuông góc với NP cắt MP tại D
a) chứng minh tam giác MND = tam giác END và ND phân giác của MNP
b) trên tia đối của tia MN, lấy điểm F sao cho MF = DP chứng minh tam giác MDF= tam giác EDP
c) minh 3 điểm E , D , F thẳng hàng
d) chứng m ND vuông góc với CF
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)a) Chứng minh NH PHb) Cho MH 4 cm; NH 3 cm. Tính MN2. Cho tam giác MNP vuông tại M, có góc N 60o và MN 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại Ea) Chứng minh: tam giác MNP tam giác ENDb) Chứng minh: tam giác MNE là tam giác đềuc) Tính độ dài cạnh PN3. Cho tam giác MNP cân tại M, góc M 30o; NP 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ 60o. Tính độ dài MQ
Đọc tiếp
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)
a) Chứng minh NH = PH
b) Cho MH = 4 cm; NH = 3 cm. Tính MN
2. Cho tam giác MNP vuông tại M, có góc N = 60o và MN = 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại E
a) Chứng minh: tam giác MNP = tam giác END
b) Chứng minh: tam giác MNE là tam giác đều
c) Tính độ dài cạnh PN
3. Cho tam giác MNP cân tại M, góc M = 30o; NP = 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ = 60o. Tính độ dài MQ
Cho tam giác MNP vuông tại M . Tia phân giác góc MNP cắt MP ở D . Kẻ DE vuông góc NP (E thuộc NP)
a) Chứng minh tam giác MND = tam giác END
b) Chứng minh MD là đường trung trực ME
c) Gọi F là giao điểm của MN và DE . Nối B với F . Chứng minh tam giác MEP cân và góc NDI qua trung điểm PF
d) Tính MD và
help mik với :<
Làm
a) Xét hai tam giác vuông NMD và tam giác vuông NED có :
ND là cạnh chung
góc MND = góc END ( gt )
Do đó : tam giác NMD = tam giác NED ( cạnh huyền - góc nhọn )
b) Theo câu a) ta có : Tam giác NMD = tam giác NED
=> +) NM = NE nên N thuộc đường trung trực của ME
+) DM = DE nên D thuộc đường trung trực của của ME
Vậy ND là đường trung trực của ME
Vì phần c của cậu sai đề ( nối B với F nhưng đề bài k có B )
Còn phần d thì chưa đủ ý để tìm đc MD
HỌC TỐT
Bài giải
Bài bạn kia làm đúng rồi nha !
Cho tam giác MNP vuông tại M. Tia phân giác của góc MNP cắt MP ở D. Kẻ DE vuông góc với NP (E\(\in\)NP)
a) Chứng minh: tam giác MND = tam giác END
b) Chứng minh: ND là đường trung trực của ME
c)Gọi K là giao điểm của MN và DE. Nối P với F. Chứng minh rằng: tam giác MNP là tam giác cân và ND đi qua trung điểm của PF
d) So sánh :MD và DP
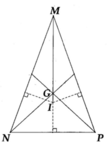
Cho tam giác MNP cân tại M có G là trọng tâm I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm M, G, I thẳng hàng.
I nằm trong tam giác và cách đều ba cạnh của tam giác nên MI là tia phân giác của góc M.
Do tam giác MNP cân tại M nên đường giác MI cũng là đường trưng tuyến.
G là trọng tâm của tam giác MNP nên G nằm trên MI.
Từ đó, suy ra M,G, I thẳng hàng.
Đúng 0
Bình luận (0)
Cho tam giác MNP cân tại M , vẽ MH vuông góc với NP
a ) Chứng minh : Tam giác MHN = Tam giác MHP
b ) Chứng minh MH là phân giác của tam giác MNP
c ) Tính MH nếu MN = 10 cm , NP = 12 cm
d ) Vẽ đường thẳng vuông góc với MN tại N và đường thẳng vuông góc với MP tại P , hai đường thẳng này cắt nhau tại K . Chứng minh M , K , H thẳng hàng .
a) xét tam giác MHN và tam giác MHP có
\(\widehat{MHN}\) = \(\widehat{MHP}\)(= 90 ĐỘ)
MN = MP ( tam giác MNP cân tại M)
MH chung
=> tam giác MHN = tam giác MHP (cạnh huyền cạnh góc vuông)
b) vì tam giác MHN = tam giác MHP (câu a)
=> \(\widehat{M1}\)= \(\widehat{M2}\)(2 góc tương ứng)
=> MH là tia phân giác của \(\widehat{NMP}\)
Đúng 0
Bình luận (0)
bạn tự vẽ hình nhé
a.
vì tam giác MNP cân tại M=> MN=MP và \(\widehat{N}\)=\(\widehat{P}\)
Xét tam giác MHN và tam giác MHP
có: MN-MP(CMT)
\(\widehat{N}\)=\(\widehat{P}\)(CMT)
MH là cạnh chung
\(\widehat{MHN}\)=\(\widehat{MHP}\)=\(^{90^0}\)
=> Tam giác MHN= Tam giác MHP(ch-gn)
=> \(\widehat{NMH}\)=\(\widehat{PMH}\)(2 GÓC TƯƠNG ỨNG) (1)
và NH=PH( 2 cạnh tương ứng)
mà H THUỘC NP=> NH=PH=1/2NP (3)
b. Vì H năm giữa N,P
=> MH nằm giữa MN và MP (2)
Từ (1) (2)=> MH là tia phân giác của góc NMP
c. Từ (3)=> NH=PH=1/2.12=6(cm)
Xét tam giác MNH có Góc H=90 độ
=>\(MN^2=NH^2+MH^2\)( ĐL Py-ta-go)
hay \(10^2=6^2+MH^2\)
=>\(MH^2=10^2-6^2\)
\(MH^2=64\)
=>MH=8(cm)
Đúng 1
Bình luận (0)
cho tam giác MNP có MN = 8 cm B = 16 cm trên cạnh MB lấy điểm E sao cho me = 4 cm đường phân giác MD của tam giác MNP cắt NE tại I (D thuộc NP)
a) Chứng minh tam giác MEN và tam giác MNP đồng dạng
b)cho MP = 20 cm Tính độ dài NE và độ dài DPDN
c)Chứng minh IE.DP= IN.DN
Cho Tam giác mnp có m cân gọi d là trung điểm đoạn thẳng np cm rằng Tam giác mnd=mpd cm mdvuoong với np![]()
Xét ΔMND và ΔMPD có
MN=MP
ND=PD
MD chung
=>ΔMND=ΔMPD
=>góc MDN=góc MDP
mà góc MDN+góc MDP=180 độ
nên góc MDN=góc MDP=180/2=90 độ
=>MD vuông góc NP
Đúng 1
Bình luận (0)



















