a) chứng minh a song song với b
b) chứng minh c vuông góc với b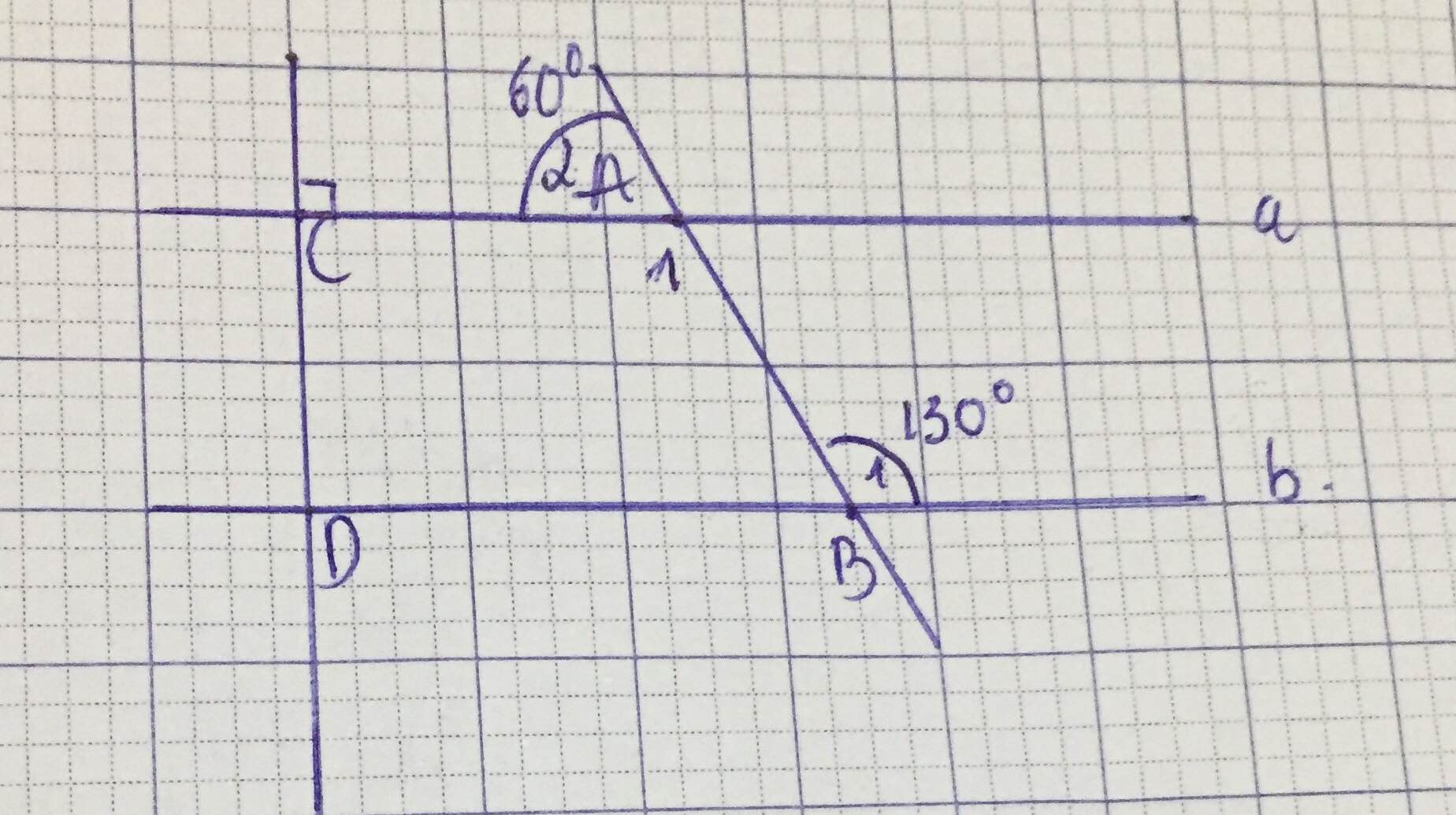

Những câu hỏi liên quan
Chứng minh nếu a song song với b, c vuông góc với a thi c vuông góc với b
CÔ LY ƠI SAO CÔ CHƯA GIAO BÀI CHO BỌN CON
cho a vuông gó với c ,b vuông góc c chứng minh a song song với b
CM theo định lí nha
GT : a⊥c;b⊥c ;a≠b
KL : a//b
Đúng 0
Bình luận (0)
Ta có: a vuông góc c tại A \(\Rightarrow\widehat{A}=90^o\)
Và b vuông góc c tại B \(\Rightarrow\widehat{B}=90^o\)
Mà: \(\widehat{A}=\widehat{B}\) lại đồng vị.
=> a//b
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC, có góc A = 70 độ. Vẽ góc B, C là góc nhọn. Vẽ BD vuông góc với AC ( D thuộc AC ), Vẽ CE vuông góc với AB ( E thuộc AB ). Vẽ Bx song song với CE, vẽ CI song song với CD, Vẽ CI song song với BD.
a. Chứng minh AB vuông góc với Bx
b. Chứng minh Ac vuông góc với CI
Cho tam giác ABC có AB = AC. M là trung điểm của BC. a) chứng minh tam giác AMB bằng tam giác AMC. b) từ M kẻ ME vuông góc với AB và MF vuông góc với AC. Chứng minh rằng AE = EF c) chứng minh EF song song với BC b) từ B kẻ đường thẳng vuông góc với AB. Từ C kẻ đường thẳng vuông góc với AC. Hai đường thẳng này cắt nhau tại N. Chứng minh rằng A,M,N thẳng hàng.
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b:Sửa đề: Chứng minh AE=AF
Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC
d: Xét ΔABN vuông tại B và ΔACN vuông tại C có
AN chung
AB=AC
Do đó: ΔABN=ΔACN
=>BN=CN
=>N nằm trên đường trung trực của BC(1)
Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,M,N thẳng hàng
Đúng 1
Bình luận (1)
Cho tam giác ABC nhọn (AB<AC). Qua A vẽ AH vuông góc với BC tại H và vẽ đường thẳng a vuông góc với AH.
a) Chứng minh rằng: Đường thaby83 a song song với BC.
b) Qua H vẽ đường thẳng b song song với AB, đường thẳng này cắt đường thẳng a tại D. Chứng minh rằng góc ABC bằng góc HDA.
c) Vẽ d là đường trung trực của cạnh AB. Chứng minh rằng: d vuông góc vởi b.
Cho hình vẽ biết tam giác ABC vuông tại A, B^=50độ AH vuông góc với BC, HK song song với AC
A, tính góc C
B, chứng minh HK vuông góc với AB
C, chứng minh: góc KHB=góc C ; góc KHB=góc BAH
a) Ta có \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o ( định lý tổng 3 góc của 1 tam giác )
90o+50o+\(\widehat{C}\) = 180o
140o+\(\widehat{C}\) = 180o
\(\widehat{C}\) = 180o-140o
\(\widehat{C}\) = 40o
b) Vì KH//AC có góc đồng vị tạo thành
Có \(\widehat{BKH}\) đồng vị với \(\widehat{BAC}\)
=> \(\widehat{BKH}\)=\(\widehat{BAC}\)=90o
=> HK vuông góc với AB
c) Ta có góc C = 40o (câu a)
Ta lại có : \(\widehat{HBK}+\widehat{BKH}+\widehat{BHK}=180^o\) (định lý tổng 3 góc của 1 tam giác)
50o+90o+\(\widehat{BHK}\) = 180o
\(\widehat{BHK}\) = 180o-(50o+90o)
=> \(\widehat{BHK}\) = 40o
Vậy góc BHK = góc C ( 40o=40o )
+ AH _|_ BC => \(\widehat{AHB}\) = 90o
Ta có \(\widehat{AHB}+\widehat{B}+\widehat{BAH}\) = 180o (định lý tổng 3 góc của 1 tam giác)
90o+50o+\(\widehat{AHB}\) = 180o
\(\widehat{AHB}\) = 180o-(90o+50o)
=> \(\widehat{AHB}\) = 40o
Vậy \(\widehat{KHB}=\)\(\widehat{AHB}\) (40o=40o)
Đúng 0
Bình luận (0)
Cho 5 đường thẳng a,,b,c,đ,ê sao cho a vuông góc với b, b song song với c, c vuông góc với d, và d song song với e
a) Có nhận xét gì về vị trí của a và c.
b) Chứng minh: a song song e
Bài 1: Cho góc xOy=60 độ, trên tia Ox lấy điểm A. kẻ tia Az sao cho xAz=60 độ. trên tia Az lấy điểm B. Kẻ tia Bd cắt Oy tại C sao cho góc CBz=120 độ. kẻ AH vuông góc với Oy và CK vuông góc với Az:
a,chứng minh: Az song song với Oy
b,chứng minh: Ox song song với Bd
c, tính góc BCO
d, chứng minh: AH song song CK
cho tam giác abc cân tại a gọi h là trung điểm của bc
a, Chứng minh AH vuông góc với BC
b, Kẻ HE vuong góc với AB tại E ; HF vuông góc với AC tại F . Chứng minh HE = HF
c, Chứng minh tam giác AEF là tam giác cân
d, Chứng minh EF song song BC




















