Cho y ∈ z, so sánh 100 . y với 0. (Chú ý: Xét mọi trường hợp của y ∈ z).

Những câu hỏi liên quan
cho y thuộc Z,so sánh 100 . y với 0
(chú ý xét mọi trường hợp của y thuộc Z)
trường hợp 1:khi y < 0 thì y là số âm . Khi đó 100 . y < 0
trường hợp 2:khi y > 0 thì y là số dương . Khi đó 100 . y > 0
trường hợp 3:khi y = 0 thì 100 . y = 0
Đúng 0
Bình luận (0)
Cho y ∈ Z, so sánh 100.y với 0
(chú ý: xét mọi trường hợp xảy ra)
Nếu y > 0 thì 100.y > 0
Nếu y = 0 thì 100.y = 0
Nếu y < 0 thì 100.y < 0
Đúng 0
Bình luận (0)
Cho \(y\in\mathbb{Z}\). So sánh \(100.y\) với \(0\)
(Chú ý : Xét mọi trường hợp của \(y\in\mathbb{Z}\))
\(y\in\mathbb{Z}\)\(y\in\mathbb{Z}\)
Vì \(y\in Z\)
=> \(\left[{}\begin{matrix}y>0\\y< 0\\y=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}100.y>0\\100.y< 0\\100.y=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1.Cho y c Z.So sánh 100.y với 0.
(Chú ý:Xét mọi trường hợp của y c Z)
2.Tìm 5 giá trị của x c Z sao cho:
a,1983.(x-7) > 0
b,(-2010).(x+3) > 0
so sánh biểu thúc M=(x-y)2(z+1)2-2(z+1)(x-y)2+(x-y)2 với số 0, với mọi x,y,z ta có biểu thức M.....0.
Chứng minh rằng :
a , với mọi x ,y thuộc Z thì [x+y]=[x]+[y]
b,với x thuộc Z , y thuộc Q thì [x+y]=x+[y]
*chú ý : [y] là phần nguyên của y
Chứng minh rằng :
a , với mọi x ,y thuộc Z thì [x+y]=[x]+[y]
b,với x thuộc Z , y thuộc Q thì [x+y]=x+[y]
*chú ý : [y] là phần nguyên của y
\(a,\left|x+y\right|\ge0\)
\(\left|x\right|+\left|y\right|\ge0\)\(\Rightarrow\left|x+y\right|=\left|x\right|+\left|y\right|\)
a,
=> | x + y | = x + y hoặc (-x )+ (-y )
vì x , y thuộc Z => | x + y | = x + y (1)
|x| + |y| = x + y (2)
từ (1) và (2) => |x + y| = |x| + | y|
Xem thêm câu trả lời
Hình 11a) biểu diễn đồ thị của các hàm số (với hệ số a 0)y 0,5x + 2;y x + 2;y 2x + 2.Hình 11b) biểu diễn đồ thị của các hàm số (với hệ số a 0):y -2x + 2;y -x + 2;y -0,5x + 2.a) Hãy so sánh các góc
α
1
,
α
2
,
α
3
và so sánh các giá trị tương ứng của hệ số a trong các hàm số (trường hợp a 0) rồi rút ra nhận xét.b) Cũng làm tương tự như câu...
Đọc tiếp
Hình 11a) biểu diễn đồ thị của các hàm số (với hệ số a > 0)y = 0,5x + 2;
y = x + 2;
y = 2x + 2.
Hình 11b) biểu diễn đồ thị của các hàm số (với hệ số a < 0):
y = -2x + 2;
y = -x + 2;
y = -0,5x + 2.
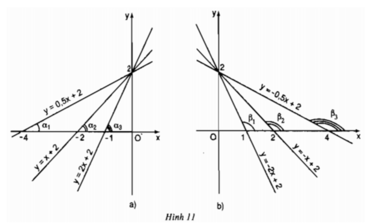
a) Hãy so sánh các góc α 1 , α 2 , α 3 và so sánh các giá trị tương ứng của hệ số a trong các hàm số (trường hợp a > 0) rồi rút ra nhận xét.
b) Cũng làm tương tự như câu a) với trường hợp a > 0.
a) Ta có: α 1 < α 2 < α 3 và các giá trị tương ứng của hệ số a trong các hàm số :
0,5 < 1 < 2
Nhận xét: Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90o
b) Ta có: β 1 < β 2 < β 3 và các giá trị tương ứng của hệ số a trong các hàm số
-2 < -1 < -0,5
Nhận xét : Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180o
Đúng 0
Bình luận (0)
Cho x thuộc tập hợp Q. So sánh [x] với x, so sánh [x] với y trong đó y thuộc tập hợp Z, y<x?














