Cho hình 13 ( sgk/Toán 8 ) trong đó ABCD là hình bình hành.Chứng minh M đối xứng với N qua C

Những câu hỏi liên quan
Cho hình vẽ, trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm c
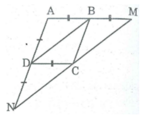
Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD( = AB ) (gt)
Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
+) Ta có AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) theo tiên đề Ơ- clit suy ra: M, C, N thẳng hàng và MC = CN( = BD).
Đúng 0
Bình luận (0)
Cho hình 13 trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm C

cho hình bình hành ABCD. Gọi M đối xứng với D qua A, N đối xứng với D qua C . Chứng minh M đối xứng với N qua B
Bài 1: cho hình bình hành ABCD. lấy điểm E đối xứng với điểm D qua A, lấy điểm F đối xứng với điểm D qua Ca, c/m: AEBC là hình bình hànhb, c/m: ABFC là hình bình hành.từ đó suy ra góc BAC góc EFDc, chứng minh điểm E và điểm F đối xứng nhau qua điểm Bđ, hình bình hành ABCD có thêm điều kiện gì thì điểm E đối xứng với điểm F qua đường thẳng BD . vẽ hình minh hoa
Đọc tiếp
Bài 1: cho hình bình hành ABCD. lấy điểm E đối xứng với điểm D qua A, lấy điểm F đối xứng với điểm D qua C
a, c/m: AEBC là hình bình hành
b, c/m: ABFC là hình bình hành.từ đó suy ra góc BAC = góc EFD
c, chứng minh điểm E và điểm F đối xứng nhau qua điểm B
đ, hình bình hành ABCD có thêm điều kiện gì thì điểm E đối xứng với điểm F qua đường thẳng BD . vẽ hình minh hoa
Cho hình bình hành ABCD,tâm O,trên OD lấy điểm E.Kẻ CF song song với AE.a Chứng minh AFCE là hình bình hànhb AF cắt BC tại M,CE cắt AD tại N.Chứng minh M,O,N thẳng hàngc Lấy K đối xứng với C qua E.Xác định vị trí của E trên OD để AKDO là hình bình hànhd Lấy I đối xứng với A qua D,H đối xứng với A qua B.Hình bình hành abcd phải có thêm điều kiện gì để I và H đối xứng với nhau qua AC
Đọc tiếp
Cho hình bình hành ABCD,tâm O,trên OD lấy điểm E.Kẻ CF song song với AE.
a Chứng minh AFCE là hình bình hành
b AF cắt BC tại M,CE cắt AD tại N.Chứng minh M,O,N thẳng hàng
c Lấy K đối xứng với C qua E.Xác định vị trí của E trên OD để AKDO là hình bình hành
d Lấy I đối xứng với A qua D,H đối xứng với A qua B.Hình bình hành abcd phải có thêm điều kiện gì để I và H đối xứng với nhau qua AC
Bài 1: Cho hình vẽ, trong đó ABCD là hình bình hành. Chứng minh rằng điểm M đối xứng với điểm N qua điểm c
Bài 2: Cho hình vẽ trong đó DE // AB, DF // AC.Chứng minh rằng điểm E đối xứng với điểm F qua điểm I.
Giúp mk vs, mai cô mk thu bài rồi!
Bài 1:

Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD( = AB ) (gt)
Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
+) Ta có AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) theo tiên đề Ơ- clit suy ra: M, C, N thẳng hàng và MC = CN( = BD).
Bài 2:

Ta có: DE //AB (gt) hay DE //AF
Và DF //AC (gt) hay DF //AE
Suy ra, tứ giác AEDF là hình bình hành.
Lại có, I là trung điểm của AD nên I cũng là trung điểm EF (tính chất hình bình hành)
Vậy E và F đối xứng qua tâm I.
Cho hình bên, trong đó ABCD là hình bình hành. Chứng minh H và K đối xứng với nhau qua điểm O
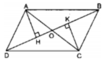
Xét hại tam giác vuông AHO và CKO, ta có:
∠ (AHO)= ∠ (CKO)= 90 0
OA = OC (tính chất hình bình hành)
∠ (AOH)= ∠ (COK)(đối đỉnh)
Suy ra: ∆ AHO = ∆ CKO (cạnh huyền, góc nhọn)
⇒ OH = OK
Vậy O là trung điểm của HK hay điểm H đối xứng với điểm K qua điểm O
Đúng 0
Bình luận (0)
cho tam giác ABC , các đường trung tuyến BN, CM gọi D là điểm đối xứng với B qua N , gọi E là điểm đối xứng C qua M
a) chứng minh các tứ giác ABCD, AEBC là hình bình hành
b) chứng minh E đối xứng với D qua A
a, Vì N là trung điểm BD và AC nên ABCD là hbh
Vì M là trung điểm CE và AB nên AEBC là hbh
b, Vì ABCD và AEBC là hbh nên \(\left\{{}\begin{matrix}AE//BC;AE=BC\\AD//BC;AD=BC\end{matrix}\right.\Rightarrow AE\equiv AD;AE=AD\)
Vậy E đx D qua A
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A. Gọi M và N lần lượt là trung điểm của AC và BC.
a) Chứng minh tứ giác AMNB là hình bình hành.
b) Gọi D là điểm đối xứng với B qua M. Chứng minh tứ giác ABCD là hình bình hành.
c) Gọi E là điểm đối xứng với A qua N. Chứng minh tứ giác ABEC là hình bình hành.
a. tam giác ABC có AM=MC và BN=NC => MN là đg TB của ABC => MN//AB => AMNB là hình thang ( k thể là Hình bình hành được )
b. D là điểm đối xứng với B qua M =>BM=MD
Tứ giác ABCD có AM=MC và BM=MD => 2 đg chéo cắt nhau tại trung điểm của mỗi đường
=> ABCD là HBH
c. E đối xứng với A qua N => AN=NE
ABEC có BN=NC và AN=NE => ABEC là HBH ( CMTT như câu b )
Đúng 0
Bình luận (0)


















