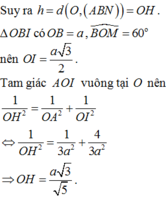Gọi A3;B5 là khối gồm những gì?.Hộp tên cho biết gì?

Những câu hỏi liên quan
Gọi
x
1
,
x
2
là hai nghiệm của phương trình
3
x
2
–
a
x
–
b
0
. Tổng
x
1
+
x
2
bằng:
(
A
)
−
a
3
(
B...
Đọc tiếp
Gọi x 1 , x 2 là hai nghiệm của phương trình 3 x 2 – a x – b = 0 . Tổng x 1 + x 2 bằng:
( A ) − a 3 ( B ) a 3 ( C ) b 3 ( D ) − b 3
Hãy chọn câu trả lời đúng
Áp dụng hệ thức Vi-et ta có:
S = x 1 + x 2 = - ( - a / 3 ) = a / 3
Vậy chọn đáp án B
Đúng 0
Bình luận (0)
Gọi
x
1
,
x
2
là hai nghiệm của phương trình
3
x
2
-
a
x
-
b
0
. Tổng
x
1
+
x
2
bằng:
(
A
)
−
a
3...
Đọc tiếp
Gọi x 1 , x 2 là hai nghiệm của phương trình 3 x 2 - a x - b = 0 . Tổng x 1 + x 2 bằng:
( A ) − a 3 ( B ) a 3 ( C ) b 3 ( D ) − b 3
Hãy chọn câu trả lời đúng
Áp dụng hệ thức Vi-et ta có:
S = x 1 + x 2 = - ( - a / 3 ) = a / 3
Vậy chọn đáp án B
Đúng 0
Bình luận (0)
Gọi a1, a2, a3, là độ dài các đường phân giác thuộc các cạnh a,b,c của tam giác ABC. CM 1/a1 + 1/a2 + 1/a3 > 1/a + 1/b + 1/c
cho 5 số nguyên a1,a2,a3,a4,a5. Gọi b1,b2,b3,b4,b5 là hoán vị của 5 số đã cho.
CMR: (a1-b1).(a2-b2).(a3-b3).(a5-b5) chia hết cho 2
Bài này lớp 6 mà bạn
Đặt c1=a1-b1, ... , c5=a5-b5.
Có c1+ c2 + ...+ c5
= (a1-b1)+(a2-b2)+...+(a5-b5)
= (a1+a2+...+a5)-(b1+b2+...+b5)
=0 (vì b1, b2, b3, b4, b5 là hoán vị của a1, a2, a3, a4, a5)
=> Trong 5 số c1,...,c5 có một số chẵn vì từ c1 đến c5 có 5 số
=> Trong các số a1-b1,...,a2-b2 có một số chẵn
Vậy ... (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho n số a1, a2, a3, ... , an mà mỗi số bằng 1 hoặc -1. Gọi Sn= a1.a2+a2.a3+a3.a4+...+an-1.an+an.a1
a) Chứng tỏ: S5 khác o
b) Chứng tỏ S6 khác 0
c) Chứng tỏ rằng: Sn=0 khi và chỉ khi n chia hết cho 4
Bài 15 : Ta gọi hai cặp góc so le ngoài là A2 và B4 ; A3 và B1
a) Vì sao nếu A1=B3 thì A2=B4;A3=B1
b) Phát biểu kết quả ở câu a)
a) Chỉ cần 1 cặp góc so le trong bằng nhau thì tất cả các cặp góc so le trong, so le ngoài đều bằng nhau.
b) Chỉ cần 1 cặp góc so le trong bằng nhau thì tất cả các cặp góc so le trong, so le ngoài, đồng vị, trong cùng phía đều bằng nhau.
Đúng 0
Bình luận (0)

(minh họa)
a,Giả sử:a//b
Vì A1 và B3 là 2 cặp góc sole ngoài(đề bài)
=>A1=B3(theo tính chất của 2 đường thẳng song song)
b,Nếu có 1 đường thẳng cắt 2 đường thẳng nào đó và tro
Lại có A2 và B4 là 2 cặp góc so le ngoài(đề bài)
=>A2=B4(theo tính chất của 2 đường thẳng song song)
b,Kết luận(phát biểu)
Nếu có 1 đường thẳng cắt 2 đường thẳng nào đó và trong các góc tạo thanh có một cặp góc sole trong,ngoài bằng nhau thì:
+Hai góc còn lại bằng nhau
+2 góc đồng vị bằng nhau
Nếu một đường thẳng cắt 2 đường thẳng song song thì:
-Hai góc sole trong/ngoài bằng nhau
-Hai góc đồng vị bằng nhau
-Hai góc trong cùng phía bằng nhau
Đúng 0
Bình luận (0)
Dựa vào đồ thị vận tốc – thời gian của chất điểm được mô tả như hình bên. Gọi
a
1
;
a
2
và
a
3
lần lượt là gia tốc chuyển động của chất điểm trên đoạn OA; AB và BC. Giá trị
a
1
+
a
2
+
a
3
bằng A. 1m/s2. B. 2m/s2. C. 0m/s2. D....
Đọc tiếp
Dựa vào đồ thị vận tốc – thời gian của chất điểm được mô tả như hình bên. Gọi a 1 ; a 2 và a 3 lần lượt là gia tốc chuyển động của chất điểm trên đoạn OA; AB và BC. Giá trị a 1 + a 2 + a 3 bằng
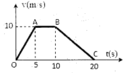
A. 1m/s2.
B. 2m/s2.
C. 0m/s2.
D. -1m/s2.
Chọn đáp án A
a 1 = 10 − 0 5 − 0 = 2 m / s 2 a 2 = 0 c h u y ể n đ ộ n g đ ề u a 3 = 0 − 10 20 − 10 = − 1 m / s 2 ⇒ a 1 + a 2 + a 3 = 1 m / s 2
Đúng 0
Bình luận (0)
Cho hình tứ diện O.ABC có đáy OBC là tam giác vuông tạiO, OBa,
O
C
a
3
. Cạnh OA vuông góc với mặt phẳng (OBC),
O
A
a
3
, gọi M là trung điểm của BC. Tính theo a khoảng cách h giữa hai đường thẳng AB và OM. A.
h
a
15
5
B. ...
Đọc tiếp
Cho hình tứ diện O.ABC có đáy OBC là tam giác vuông tạiO, OB=a, O C = a 3 . Cạnh OA vuông góc với mặt phẳng (OBC), O A = a 3 , gọi M là trung điểm của BC. Tính theo a khoảng cách h giữa hai đường thẳng AB và OM.
A. h = a 15 5
B. h = a 3 2
C. h = a 3 15
D. h = a 5 5
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A,
A
B
a
,
A
C
a
3
.
Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) là trung điểm H của BC,
A
H
a
3
.
Gọi
φ
là góc giữa hai đường thẳng A’B và B’C. Tính
c
o
s...
Đọc tiếp
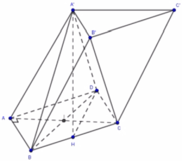
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, A B = a , A C = a 3 . Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) là trung điểm H của BC, A ' H = a 3 . Gọi φ là góc giữa hai đường thẳng A’B và B’C. Tính c o s φ .
A. c o s φ = 1 2 .
B. c o s φ = 6 8 .
C. c o s φ = 6 4 .
D. c o s φ = 3 2 .
Đáp án B.
Phương pháp:
Sử dụng công thức Côsin:
a 2 = b 2 + c 2 − 2 b c cos A
Cách giải:
Dựng hình bình hành ABCD (tâm I). Khi đó, A’B’CD là hình bình hành (do A ' B ' → = A B → = D C → )
⇒ A ' D / / B ' C ⇒ A ' B ; B ' C = A ' B ; A ' D
Tam giác ABC vuông tại A
⇒ B C = A B 2 + A C 2 = a 2 + a 3 2 = 2 a
H là trung điểm của BC
⇒ H B = H C = a
Tam giác A’BH vuông tại H
⇒ A ' B = A ' H 2 + H B 2 = a 3 2 + a 2 = 2 a
Tam giác ABC vuông tại A
⇒ cos A B C = A B B C = a 2 a = 1 2
ABCD là hình bình hành
⇒ A B / / C D ⇒ D C B = 180 0 − A B C ⇒ cos D C B = − c osABC=- 1 2
Tam giác BCD:
B D = B C 2 + C D 2 − 2 B C . C D . cos D C B = 2 a 2 + a 2 − 2.2 a . a . − 1 2 = a 7
Tam giác CDH:
D H = C H 2 + C D 2 − 2 C H . C D . cos D C B = a 2 + a 2 − 2 a . a . − 1 2 = a 3
Tam giác A’DH vuông tại H:
A ' D = A ' H 2 + H D 2 = a 3 2 + a 3 2 = a 6
Tam giác A’BH:
cosBA ' D = A ' D 2 + A ' B 2 − B D 2 2 A ' D . A ' B = a 6 2 + 2 a 2 − 7 a 2 2. a 6 .2 a = 3 4 6 = 6 8 .
Đúng 0
Bình luận (0)