Đáp án D

Dễ có số cách chọn 3 điểm từ 11 điểm đã cho là :  C 11 3   =   165

Để 3 điểm được chọn tạo thành một tam giác thì phải thỏa mãn 3 điểm đó không thẳng hàng. Do đó có hai trường hợp xảy ra :

-   Thứ nhất có hai điểm trên đường thẳng a và một điểm trên đường thẳng b

-   Thứ hai có một điểm trên đường thẳng a và hai điểm trên đường thẳng b

Từ đây suy ra số cách chọn 3 điểm để tạo thành một tam giác là :  C 6 2 C 5 1   +   C 6 1 C 5 2   =   135

Vậy xác suất cần tìm là 135 165   =   9 11 . => Chọn đáp án D.

Đáp án D

Dễ có số cách chọn 3 điểm từ 11 điểm đã cho là :  C 11 3 = 165

Để 3 điểm được chọn tạo thành một tam giác thì phải thỏa mãn 3 điểm đó không thẳng hàng. Do đó có hai trường hợp xảy ra :

-        Thứ nhất có hai điểm trên đường thẳng a và một điểm trên đường thẳng b

-        Thứ hai có một điểm trên đường thẳng a và hai điểm trên đường thẳng b

Từ đây suy ra số cách chọn 3 điểm để tạo thành một tam giác là :  C 6 2 C 5 1 + C 6 1 C 5 2 = 135

Biến cố A : "ba điểm tạo thành tam giác", tức là ba điểm không thẳng hàng.

Có 2 trường hợp:

- Hai điểm thuộc a và một điểm thuộc b có  C 6 2 . C 5 1  cách

- Hai điểm thuộc b và một điểm thuộc a có C 6 1 . C 5 2  cách

Suy ra,số phần tử của biến cố A là: 

Ω A = C 6 2 . C 5 1 + C 6 1 . C 5 2 = 135

Đáp án A.

a. 3 điểm kẻ được 3 đoạn thẳng

b. 5 điểm vẽ được 8 đoạn thẳng

c. 7 điểm vẽ được 15 đoạn thẳng

d. n điểmvẽ được ................................................................................................( ko biết nữa)

a. 3 điểm kẻ được 3 đoạn thẳng

b. 5 điểm vẽ được 8 đoạn thẳng

c. 7 điểm vẽ được 15 đoạn thẳng

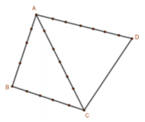
TH1: Tam giác được tạo thành từ 2 điểm thuộc một cạnh và điểm thứ ba thuộc một trong ba cạnh còn lại.

Có

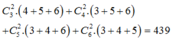
tam giác.

TH2: Tam giác được tạo thành từ ba đỉnh thuộc ba cạnh khác nhau.

Có

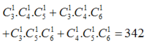
 tam giác.

Vậy có 439 + 342 = 781  tam giác.

Chọn A.

Lời giải:

$\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}, \overrightarrow{AE}$

$\overrightarrow{BA}, \overrightarrow{BC}, \overrightarrow{BD}, \overrightarrow{BE}$

$\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{CD}, \overrightarrow{CE}$

$\overrightarrow{DA}, \overrightarrow{DB}, \overrightarrow{DC}, \overrightarrow{DE}$

$\overrightarrow{EA}, \overrightarrow{EB}, \overrightarrow{EC}, \overrightarrow{ED}$

Chọn đáp án B

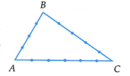
Có C 18 3  cách lấy ra 3 điểm từ 18 điểm.

Để tạo thành tam giác thì 3 điểm lấy ra phải là 3 điểm không thẳng hàng. Do đó ta trừ đi số các bộ 3 điểm thẳng hàng (lấy trên các cạnh AB, BC, CD, DA).

Vậy số tam giác được tạo thành là 

a, tia AB,AC,AD,AE

        BC,BD;BE

        CD,CE

       DE

\(\Rightarrow\)CÓ 10 tia.

b,theo đề bài ta có:

\(\frac{n\times\left(n-1\right)}{2}=132\)

\(\Leftrightarrow n\times\left(n-1\right)=264\)

\(\Rightarrow n\times\left(n-1\right)=\)

hình như đề bj sai bn ạ !sửa 132 tia của đề thành 66 tia thì n=12 nha 

sau khi sửa đề nè bn:

:\(\frac{n\times\left(n-1\right)}{2}=66\)

\(\Leftrightarrow n\times\left(n-1\right)=132\)

\(\Leftrightarrow n\times\left(n-1\right)=12\times11\)

\(\Rightarrow n=12\)