viết phương trình mặt cầu (S) có tâm I (3;-4;2) và tiếp xúc với mặt phẳng OXY

Những câu hỏi liên quan
viết phương trình mặt cầu (S) có tâm I (3;-4;2) và tiếp xúc với mặt phẳng Oxy
Do (S) tiếp xúc Oxy \(\Rightarrow R=\left|z_I\right|=2\)
Phương trình (S):
\(\left(x-3\right)^2+\left(y+4\right)^2+\left(z-2\right)^2=4\)
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz cho mặt cầu (S) có tâm I(1;-2;3) và đường thẳng d có phương trình
x
1
+
2
t
y
-
1
-
t...
Đọc tiếp
Trong không gian tọa độ Oxyz cho mặt cầu (S) có tâm I(1;-2;3) và đường thẳng d có phương trình x = 1 + 2 t y = - 1 - t z = 1 + 2 t . Biết rằng mặt cầu (S) tiếp xúc với đường thẳng d. Viết phương trình mặt cầu (S).
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S). A.
x
2
+
y
2
+
z
-
3
2
9
B.
x
2
+
y
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
A. x 2 + y 2 + z - 3 2 = 9
B. x 2 + y 2 + z + 3 2 = 9
C. x - 3 2 + y 2 + z 2 = 3
D. x - 3 2 + y 2 + z 2 = 9
Chọn D.
Phương pháp: Tìm tâm và bán kính mặt cầu.

Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I nằm trên tia Ox bán kính bằng 3 và tiếp xúc với mặt phẳng (Oyz). Viết phương trình mặt cầu (S).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S). A.
(
x
-
1
)
2
+
(
y
+
1
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 = 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S).
A. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 13
B. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 169
C. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169
D. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169
Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S). A.
(
S
)
:
x
2
+
(
y
+...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 = 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S).
A. ( S ) : x 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 3
B. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 1
C . ( S ) : x 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 3
D. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 2
Chọn C
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3
Đúng 0
Bình luận (0)
Cho I(4;-4;1). Viết phương trình mặt cầu (S) tâm I sao cho (S) cắt mặt phẳng (Oxy) theo một đường tròn có bán kính
r
2
.
Đọc tiếp
Cho I(4;-4;1). Viết phương trình mặt cầu (S) tâm I sao cho (S) cắt mặt phẳng (Oxy) theo một đường tròn có bán kính r = 2 .
![]()
![]()
![]()
![]()
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là: A.
(
x
-
1
)
2
+
(
y
-
...
Đọc tiếp
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R=3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là:
A. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 9
B. ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
C. x 2 + y 2 + z 2 - 2x - 4y + 2z - 3 = 0
D. x 2 + y 2 + z 2 = 9
Đáp án B
Mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ nên mặt cầu (S’) có tâm I’(-1;-2; 1) đối xứng với I qua gốc O và có bán kính R’ = R = 3.
Phương trình mặt cầu (S’) là: ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
Đúng 0
Bình luận (0)
Viết phương trình mặt cầu (S) có tâm I nằm trên tia Oy, bán kính R 4 và tiếp xúc với mặt phẳng (Oxz) A.
x
2
+
y
2
+
z
−
2
2
16.
B.
x
2
+
y
+
4
+
z...
Đọc tiếp
Viết phương trình mặt cầu (S) có tâm I nằm trên tia Oy, bán kính R = 4 và tiếp xúc với mặt phẳng (Oxz)
A. x 2 + y 2 + z − 2 2 = 16.
B. x 2 + y + 4 + z 2 = 16.
C. x 2 + y − 4 + z 2 = 16.
D. x 2 + y ± 4 + z 2 = 16.
Đáp án C.
Ta có I ∈ O y ⇒ I 0 ; i ; 0 , i > 0.
O x z : y = 0 ⇒ d I ; O x z = R = 4 ⇔ i 4 = 4 ⇒ i = 4 ⇒ I 0 ; 4 ; 0 ⇒ x 2 + y − 4 + z 2 = 16.
Đúng 0
Bình luận (0)
Cho mặt cầu (S) có tâm I(2;1;-1) và tiếp xúc với mặt phẳng (
α
) có phương trình 2x-2y-z +3 0. Bán kính mặt cầu (S) là A.
2
9
B. 2 C.
2
3
D.
4
3
Đọc tiếp
Cho mặt cầu (S) có tâm I(2;1;-1) và tiếp xúc với mặt phẳng ( α ) có phương trình 2x-2y-z +3 = 0. Bán kính mặt cầu (S) là
A. 2 9
B. 2
C. 2 3
D. 4 3
Đáp án B
Ta có: bán kính mặt cầu tâm I tiếp xúc với mặt phẳng ( α ) là khoảng cách từ I đến mặt phẳng
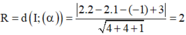
Đúng 0
Bình luận (0)