Tìm giá trị nhỏ nhất của biểu thức sau :
N = 2x^2 - 2x + 4xy - 6y + 10y^2 + 2015
Tìm giá trị nhỏ nhất của biểu thức sau:
x^2 + 5y^2 + 2x - 4xy. - 10y + 14
tìm giá trị nhỏ nhất của các biểu thức
A=2x^2-10x+17
B=(x-1)(x+2)(x+3)(x+6)
C=5x^2+y^2+10+4xy-14x-6y
D=2x^2+2y^2+26+12x-8y
E=5x^2+10y^2+26-14xy-18x-28y
Tìm GTNN cuả đa thức:2x^2-2x+4xy-6y+10y^2+2015
Tìm giá trị lớn nhất của biểu thức : A= -2x^2-10y^2+4xy+4x+4y+2016
Tìm giá trị lớn nhất của biểu thức: A= -2x^2-10y^2+4xy+4x+4y+2016
\(A=-2x^2+4xy-2y^2+4\left(x-y\right)-2-8y^2+8y+2019\\ A=\left[-2\left(x-y\right)^2+4\left(x-y\right)-2\right]-8\left(y^2-y+\dfrac{1}{4}\right)+2020\\ A=-2\left(x-y-1\right)^2-8\left(y-\dfrac{1}{2}\right)^2+2020\le2020\\ A_{max}=2020\Leftrightarrow\left\{{}\begin{matrix}x-y=1\\y=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1+\dfrac{1}{2}=\dfrac{3}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
tìm giá trị lón nhất của biểu thức A= -2x^2-10Y^2+4XY+4X+4Y+2013
Tìm giá trị nhỏ nhất của biểu thức Q= x2+2y2+2xy - 2x - 6y +2015
\(Q=x^2+2y^2+2xy-2x-6y+2015\)
\(Q=x^2+2x\left(y-1\right)+2y^2-6y+2015\)
\(Q=x^2+2x\left(y-1\right)+y^2-2y+1+y^2-4y+4+2010\)
\(Q=x^2+2x\left(y-1\right)+\left(y-1\right)^2+\left(y-2\right)^2+2010\)
\(Q=\left(x+y-1\right)^2+\left(y-2\right)^2+2010\ge2010\forall x;y\)
Dấu "=" xảy ra khi x=-3;y=4
\(Q=x^2+2y^2+2xy-2x-6y+2015\)
\(Q=\left(x^2+y^2+1+2xy-2x-2y\right)+\left(y^2-4y+4\right)+2010\)
\(Q=\left(x+y-1\right)^2+\left(y-2\right)^2+2010\ge2010\)
Dâu'=' xảy ra khi và chỉ khi
\(\hept{\begin{cases}x+y-1=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-1\\y=2\end{cases}}}\)
Vậy giá trị nhỏ nhất của Q bằng 2010, xảy ra khi x=-1,y=2
Tìm giá trị nhỏ nhất của biểu thức: Q = x 2 + 2 y 2 + 2 x y − 2 x − 6 y + 2015
Q = x 2 + 2 y 2 + 2 x y − 2 x − 6 y + 2015 = x 2 + 2 x y + y 2 − 2 x − 2 y + 1 + y 2 − 4 y + 4 + 2010 = x 2 + 2 x y + y 2 − 2 x + 2 y + 1 + y 2 − 4 y + 4 + 2010 = x + y 2 − 2 x + y + 1 + y 2 − 4 y + 4 + 2010 = x + y − 1 2 + y − 2 2 + 2010
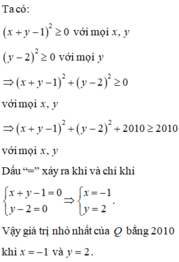
tìm giá trị nhỏ nhất của biểu thức sau A=x^2-2xy+2y^2+2x-10y+2033
\(A=x^2-2xy+y^2+2x-2y+1+y^2-8y+16+2016\)
\(A=\left(x-y\right)^2+2\left(x-y\right)+1+\left(y-4\right)^2+2016\)
\(A=\left(x-y+1\right)^2+\left(y-4\right)^2+2016\)
vì \(\left(x-y+1\right)^2\ge0\)
\(\left(y-4\right)^2\ge0\)
nên \(\left(x-y+1\right)^2+\left(y-4\right)^2+2016\ge2016\)
dấu bằng xảy ra \(\Leftrightarrow\hept{\begin{cases}x=3\\y=4\end{cases}}\)
vậy gtnn của bt là 2016 khi x=3;y=4
đề này của sở giáo dục và đào tạo tỉnh hà nam
mk chiu ban ak di thi mk cug vao caau day nhưng ko biet lam