Tìm ba số dương biết tổng các bình phương của chúng bằng 181;số thứ hai bằng \(\dfrac{3}{4}\) số thứ nhất và bằng \(\dfrac{2}{3}\) số thứ ba

Những câu hỏi liên quan
Tìm 3 số dương , biết rằng tổng các bình phương của chúng bàng 181 , số thứ 2 bằng 3/4 số thứ nhất và bằng 2/3 số thứ ba
Bài toán là :
Tìm 3 số dương , biết tổng các bình phương của chúng = 181 ; và số thứ hai bằng 3/4 số thứ nhất và bằng 2/3 số thứ ba .
Gọi ba số dương cần tìm là x , y , z
Theo đề bài ra ta có : x2 + y2 + z2
và y = 3.x/4 = 2.z/3
BCNN(3;2) = 6
suy ra : y . 1/6 = 1/6 . 3/4 .x = 1/6 . 2/3 . z
khi và chỉ khi : y/6 = x/8 = x/9
suy ra : y2/62 = x2/82 = z2/92 = y2 + x2 + z2/36 + 64 + 81= 181/181= 1
Từ y2/62 = 1 suy ra y2 = 62 suy ra y = 6
x2/82 = 1 suy ra x2 = 82 suy ra x = 8
z2/92 = 1 suy ra z2 = 92 suy ra z = 9
Vậy y = 6 ; x = 8 ; z = 9
Đúng 0
Bình luận (0)
Tìm ba số dương , biết tổng các bình phương của chúng = 181, số thứ hai bằng \(\frac{3}{4}\) số thứ nhất và bằng \(\frac{2}{3}\) số thứ ba.
tìm 3 số dương biết tổng của các bình phương của chúng bằng 181 số thứ hai bằng 3 phần 4 số thứ nhất và bằng 2 phaàn 3 số thứ 3
giup vs
Tìm công sai dương của cấp số cộng ba số hạng, biết tổng của chúng bằng 9 và tổng bình phương bằng 125.
A. 7
B. 8
C. 9
D. 10
Chọn A
Gọi d là công sai. Ba số phải tìm là: (x-d); x; (x+d). Ta có hệ phương trình
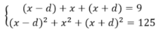
![]()
Đúng 0
Bình luận (0)
tìm 3 số dương biết tổng các bình phương của chúng bằng 180. Số thứ hai bằng 3/4 số thứ nhất và bằng 2/3 số thứ ba.
Tìm ba số dương biết tổng bình phương của chúng bằng 481 . Biết số thứ hai bằng 4/3 số thứ nhất và bằng 3/4 số thứ ba
Tìm 3 số dương biết tổng bình phương của chúng bằng 481. Biết số thứ hai bằng 4/3 số thứ nhất và bằng 3/4 số thứ ba
tìm số chẵn dương liên tiếp biết tổng các bình phương của chúng bằng 164
gọi hai số chãn dương liên tiếp là \(a\)và \(a+2\)trong đó \(\left(a>0\right)\)
theo giả thiết thì \(a^2+\left(a+2\right)^2=164\)
<=> \(a^2+a^2+4a+4=164\)
=> \(2a^2+4a-160=0\)
=> \(\left(a-8\right)\left(a+10\right)=0\)=> \(\hept{\begin{cases}a=8\left(tm\right)\\a=-10< 0\left(ktm\right)\end{cases}}\)
Tìm 7 số nguyên dương sao cho tích các bình phương của chúng bằng 2 lần tổng các bình phương của chúng.














