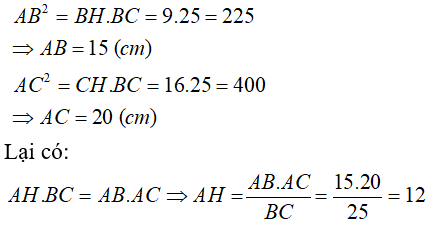Bài 9 với ah
Bài 9 với ah

Những câu hỏi liên quan
Bài 1 : Cho tam giác ABC vuông tại A , đường cao AH , có HB =9 cm , HC =16cm . Tính góc B và góc C
GIẢI GIÚP MÌNH BÀI NÀY VỚI Ạ , MÌNH ĐANG CẦN GẤP
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=9\cdot25=225\\AC^2=16\cdot25=400\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
Đúng 1
Bình luận (0)
Bài 1 cho tam giác ABC vuông tại A , AH vuông góc với BC tại H , AH =30 cm , HB:HC=5:6 . Tính AB BC AC
Bài 2 cho tam giác ABC vuông tại A , AH vuông góc với BC tại H . AB20 cm HC=9 cm Tính AH
MÌNH ĐANG CẦN GẤP TRONG TỐI NAY MONG CÁC BẠN GIÚP ĐỠ. XIN CHÂN THANH CAM ON VA HAU TA
hình tự vẽ nhé:
Áp dụng hệ thức lượng ta có:
\(AC^2=HC.BC=9BC\)
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(400+9BC=BC^2\)
\(\Leftrightarrow\)\(BC^2-9BC-400=0\)
\(\Leftrightarrow\)\(\left(BC-25\right)\left(BC+16\right)=0\)
\(\Leftrightarrow\)\(BC=25\)
\(\Rightarrow\)\(AC^2=9.25=225\)
\(\Rightarrow\)\(AC=\sqrt{225}=15\)
Áp dụng hệ thức lượng ta có:
\(AB.AC=AH.BC\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}\)
\(\Rightarrow\)\(AH=\frac{20.15}{25}=12\)
Đúng 0
Bình luận (0)
48 phút 36 giây : 9 + 9,54 phút=............. mọi người giúp em bài này với ah, em đg cần gấp ah,ai làm nhanh em sẽ tick
48,6phút:9+9,54phút
5,4phút+9,54phút
14,94phút
[ 48 phut 36 giay : 9 ] + 9,54 phut = 5phut 24 giay + 9,54 phut = 5,4 phut + 9,54 phut = 14,94 phut
48 phút 36 giây : 9 + 9,54 phút
= 5 phút 24 giây + 9,54 phút
= 5,4 phút + 9,54 phút
= 14,94 phút
CÂU TRẢ LỜI ĐÂY NHA !
CHÚC BẠN HỌC GIỎI !
Xem thêm câu trả lời
Bài 9: Cho hình chữ nhật ABCD có AB = 8 cm; BC = 6 cm. Vẽ đường cao AH của tam giác ADB.
a) Chứng minh DAHB đồng dạng với DBCD.
b) Tính độ dài đoạn thẳng AH .
c) Tính diện tích DAHB
a: Xet ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó: ΔAHB\(\sim\)ΔBCD
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(AH=\dfrac{AB\cdot AD}{BD}=4,8\left(cm\right)\)
c: \(HB=\dfrac{AB^2}{BD}=6,4\left(cm\right)\)
\(S=\dfrac{AH\cdot HB}{2}=2,4\cdot6,4=15,36\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Bài 3: Cho tam giác ABC vuông tại A có AH là đường cao, BH = 9 cm, CH = 16 cm. Tính BC, AH, AB, AC
Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E của H trên AB, AC
a, Cho CH= 4, BH=9. Tính DC
b, Chứng minh AD.AB=AE.AC
c, Chứng minh BC.BD.CE=AH*3
Ai giúp mình làm bài này với
Bài 7: Cho tam giác AB cân tại A, kẻ AH vuông góc với BC tại H. Lấy điểm D, E lần lượt thuộc các đoạn thẳng HB và HC sao cho BDCE. So sánh độn dài đoạn thẳng AD, AE.Bài 9: Cho tam giác ABC vuông tại A và góc B lớn hơn góc C. Kẻ AH vuông góc với BC tại H. Trên tia BH lấy điểm D sao chp H là trung điểm của BD. Gọi E là hình chiếu của D trên đường thẳng AC, K là hình chiếu của C trên đường thẳng AD. Chứng minh rằng: a) Điểm D nằm trên đoạn thẳng HC. b) DEDK.
Đọc tiếp
Bài 7: Cho tam giác AB cân tại A, kẻ AH vuông góc với BC tại H. Lấy điểm D, E lần lượt thuộc các đoạn thẳng HB và HC sao cho BD=CE. So sánh độn dài đoạn thẳng AD, AE.
Bài 9: Cho tam giác ABC vuông tại A và góc B lớn hơn góc C. Kẻ AH vuông góc với BC tại H. Trên tia BH lấy điểm D sao chp H là trung điểm của BD. Gọi E là hình chiếu của D trên đường thẳng AC, K là hình chiếu của C trên đường thẳng AD. Chứng minh rằng: a) Điểm D nằm trên đoạn thẳng HC.
b) DE=DK.
1:
Xét ΔABD và ΔACE có
AB=AC
góc B=góc C
BD=CE
=>ΔABD=ΔACE
=>AD=AE
2:
a: H là trung điểm của DB
=>D thuộc tia đối của tia HB
=>D thuộc HC
b: góc KCD=góc DAH
góc DAH=góc CED
=>góc KCD=góc CED
Xét ΔCED vuông tại E và ΔCKD vuông tại K có
CD chung
góc ECD=góc KCD
=>ΔCED=ΔCKD
=>DE=DK
Đúng 0
Bình luận (0)
Bài 4: Cho ∆ABC vuông tại A , đường cao AH=48cm. Biết
BH:CH = 9:16. Tính AB, AC?
Bài 5: Cho tam giác ABC đều có cạnh là a, đường cao AH. Tia phân
giác của ABC ̂ cắt AH tại I. Tính theo a
a)Độ dài AH b)Độ dài IH
Cho tam giác ABC vuông tại A, AB = 3, AC = 4. Đường cao AH và đường trung tuyến AM. Xét vị trí tương đối của các điểm B, A,M,C đối với đường tròn (m;9/5)
Làm giúp mik bài này với ạ