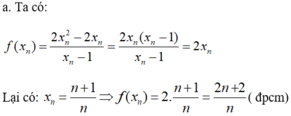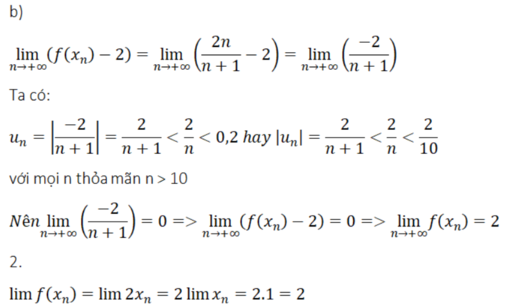Xin xn
Những câu hỏi liên quan
Xin xn
Xem thêm câu trả lời
cho dãy (xn) thỏa mãn x1=1
xn+1 - căn(xn+1) = xn + căn(xn) + 1/(n+4)
tính lim(xn/(n2))
- Qủa gì mà chua chua thế?Xin thưa rằng quả khế.-Qủa gì mà da cưng cứng?Xin thưa rằng quả trứng-Qủa gì mặc bao nhiêu áo?Xin thưa rằng quả táo-Qủa gì mà lăn lông lốc?Xn thưa rằng quả bóng-Qủa gì mà gai chin chít?Xin thưa rằng quả mít-Qủa gì mà to to nhất?Xin thưa rằng quả đấtXếp loại quả vào 2 loại sau1.Bộ phận của cây do bầu nhụy hoa phát triển mà thành,bên trong có chứa hạt:2.Từ dùng để chỉ những vật có hình giống như quả cây
Đọc tiếp
- Qủa gì mà chua chua thế?Xin thưa rằng quả khế.
-Qủa gì mà da cưng cứng?Xin thưa rằng quả trứng
-Qủa gì mặc bao nhiêu áo?Xin thưa rằng quả táo
-Qủa gì mà lăn lông lốc?Xn thưa rằng quả bóng
-Qủa gì mà gai chin chít?Xin thưa rằng quả mít
-Qủa gì mà to to nhất?Xin thưa rằng quả đất
Xếp loại quả vào 2 loại sau
1.Bộ phận của cây do bầu nhụy hoa phát triển mà thành,bên trong có chứa hạt:
2.Từ dùng để chỉ những vật có hình giống như quả cây
1.Bộ phận của cây do bầu nhụy hoa phát triển mà thành,bên trong có chứa hạt:
=>Quả ( táo, khế,mít)
2.Từ dùng để chỉ những vật có hình giống như quả cây
=> quả bóng , quả đất, quả trứng.
Đúng 0
Bình luận (0)
Bài 4: Làm tính nhân
a) xn. yn+2.(xy+x2y+1)
b) (4xn-2+xn+1).xn
c) 4xy.(xn-2 yn+1+ xn yn+1)
xin cac ban day tra loi giup mk voi nghi cach lam luon nh
Xem chi tiết
142,29 \(chia\)9 718,128 chia 8 mk xn day cac ban chua bao gio tra loi cau cua mk ca ai dung tui tik
Mình nghĩ câu hỏi của bạn bị sai đề rồi đó
Đúng 0
Bình luận (0)
tim cac so x1,x2,...,xn-1 ,xn biet rang x1/a1=x2/a2=...=xn/an va x1+x2+...+xn=c
vao thong tin tai khoan o cho hinh tam giac ben canh ten cua ban roi an vao doi anh hien thi .xong
Đúng 0
Bình luận (0)
Cho dãy (xn) thỏa 1<xn<2 và xn+1=1+xn-1/2xn^2 với mọi n thuộc N
a,chứng minh |xn-căn 2|<(1/2)^n với mọi n lớn hơn hoặc bằng 3
b,Tính lim xn
Cho xn vào 1 team vs ạ! Xin hứa sẽ nghiêm túc chấp hành mọi nội quy... và sẽ cùng nhau tiến bộ>....<!
Câu hỏi: Chứng minh rằng 3 số tự nhiên chia hết cho 3.(Biết làm r nhưng nếu bạn nào lm đúng vẫn tik vì ko lại nêu nội quy ra:D)
Bài làm
Gọi ba số tự nhiên liên tiếp là: x, x + 1, x + 2
Ta có: x + x + 1 + x + 2
= ( x + x + x ) + ( 1 + 2 )
= 3x + 3
= 3( x + 1 ) chia hết cho 3
Vậy 3 số tự nhiên liên tiếp chia hết cho 3 ( đpcm )
# Học tốt #
Xét hàm số
f
x
2
x
2
-
2
x
x
-
1
1. Cho biến x những giá trị khác 1 lập thành dãy số
x
n
,
x
n...
Đọc tiếp
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:
Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
