a: Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC

Do đó: ΔAIB=ΔAIC

a)  Xét  \(\Delta HAC\) và       \(\Delta ABC\) có:

\(\widehat{AHC}=\widehat{BAC}=90^0\)

\(\widehat{C}\)   CHUNG

suy ra:    \(\Delta HAC~\Delta ABC\)

b)  Áp dụng định lý Pytago vào tam giác vuông ABC ta có:

       \(BC^2=AB^2+AC^2\)

\(\Leftrightarrow\)  \(BC^2=6^2+8^2=100\)

\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)

 \(\Delta HAC~\Delta ABC\)   \(\Rightarrow\)\(\frac{AH}{AB}=\frac{AC}{BC}\)

hay    \(\frac{AH}{6}=\frac{8}{10}\)   \(\Rightarrow\) \(AH=\frac{6.8}{10}=4,8\)

mik làm dc câu a vs b giống bạn à 2 câu khi kh biết làm

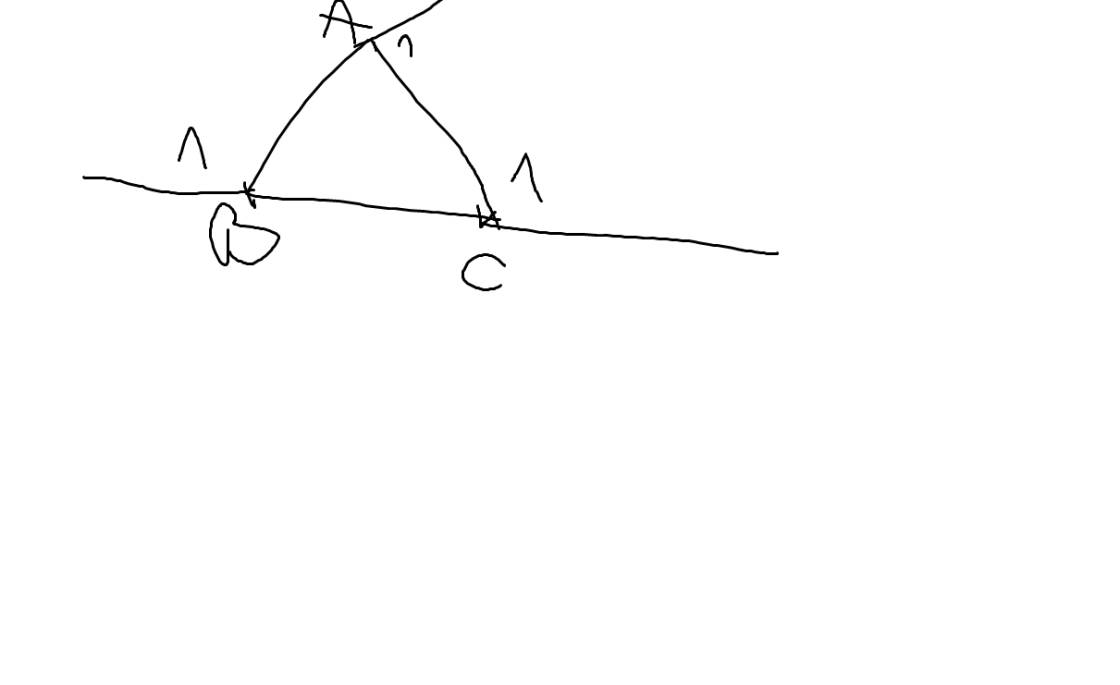
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC

Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)

=>\(\widehat{B_1}=180^0-\widehat{ABC}\)

\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)

=>\(\widehat{C_1}=180^0-\widehat{ACB}\)

\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)

=>\(\widehat{A_1}=180^0-\widehat{BAC}\)

\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)

\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)

\(=540^0-180^0=360^0\)

Để chứng minh công thức AB+AC-BC = 2AE, ta sẽ sử dụng định lí phân giác trong tam giác:

Ta có: BOC là phân giác góc B và C, do đó BO và CO cắt nhau tại O, chia góc BOC thành hai góc bằng nhau. Khi đó, ta có: AOE và AOD là cặp tam giác đồng dạng, vì chúng có: Cặp góc vuông: ∠AOE = 90^o và ∠AOD = 90^o Cặp góc bằng nhau: ∠OAE = ∠OAD (vì AE là phân giác góc A) Do đó: cặp góc còn lại cũng bằng nhau: ∠AEO = ∠ADO Từ đó suy ra: các tam giác AOE và AOD đồng dạng theo nguyên tắc cạnh - góc - cạnh (góc AEO hoặc ADO là góc chung, AE = AD và EO = OD): => AE/EO = AD/OD Đặt x = EO. Khi đó, OD = x/BC và AE = x/AB (do AE là phân giác góc A). Áp dụng công thức phân giác để tính x theo AB, AC và BC: Xét tam giác EOx: áp dụng định lí cosin trong tam giác vuông EOX có: OE^2 = OX^2 + EX^2 AB^2 + BE^2 = (AB-BC)^2 + x^2 AC^2 + CD^2 = (AC-BC)^2 + x^2 suy ra: 2x^2 = AB^2 + AC^2 - BC^2 Thay x bằng giá trị tương ứng, ta được: (AB+AC-BC)/2 = AE Vậy, ta đã chứng minh được công thức cần tìm.

lớp 7 chưa có lượng giác bạn ơi

a) DB/DC=8/6=4/3                               

giúp mik ik mn

a: Xét ΔMAB và ΔMEC có

MA=ME

\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)

MB=MC

Do đó: ΔMAB=ΔMEC

b: Sửa đề: AB//EC

Ta có: ΔMAB=ΔMEC

=>\(\widehat{MAB}=\widehat{MEC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//CE

c: Ta có: AB//CE

AB\(\perp\)AC

Do đó: CE\(\perp\)CA

Xét ΔECA vuông tại C và ΔBAC vuông tại A có

EC=BA

AC chung

Do đó: ΔECA=ΔBAC

=>EA=BC

Xét ΔMAC và ΔMEB có

MA=ME

\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)

MC=MB

Do đó ΔMAC=ΔMEB

=>AC=BE

Xét ΔBEC và ΔCAB có

BE=CA

EC=AB

BC chung

Do đó: ΔBEC=ΔCAB

=>\(\widehat{BEC}=\widehat{CAB}=90^0\)

=>ΔBEC vuông tại E