vô câu hỏi tương tự có nhé idol , đăng bài bị trùng rồi xD

Harley chuyên Lam Sơn mới thi thì làm gì có chuyện trùng được bro(:

https://olm.vn/hoi-dap/detail/428406019268.html đui à bro ? =)

Giả sử tồn tại số \(p\)thỏa mãn. 

Ta đặt \(\frac{p^2-p-2}{2}=a^3\).

- \(p=2\)thỏa mãn.

- \(p>2\)do là số nguyên tố nên \(p\)lẻ.

Ta có: \(\frac{p^2-p-2}{2}=a^3\Leftrightarrow p\left(p-1\right)=2\left(a+1\right)\left(a^2-a+1\right)\)suy ra \(p\)là ước của \(a+1\)hoặc \(a^2-a+1\).

+) \(p|a+1\): \(\frac{p^2-p-2}{2}=a^3\)suy ra \(a< p\Rightarrow a+1=p\).

Thế vào cách đặt ban đầu ta được \(\frac{\left(a+1\right)^2-\left(a+1\right)-2}{2}=a^3\Leftrightarrow2a^3-a^2-a+2=0\)

\(\Leftrightarrow a=-1\)không thỏa. 

+) \(p|a^2-a+1\): Đặt \(a^2-a+1=kp\)(1).

\(p\left(p-1\right)=2\left(a+1\right)\left(a^2-a+1\right)=2\left(a+1\right)kp\)

\(\Rightarrow p-1=2\left(a+1\right)k\Leftrightarrow p=2k\left(a+1\right)+1\)thế vào (1): 

\(a^2-a+1=k\left[2k\left(a+1\right)+1\right]\)

\(\Leftrightarrow a^2-\left(2k^2+1\right)a-2k^2-k+1=0\)

\(\Delta=\left(2k^2+1\right)^2-4\left(-2k^2-k+1\right)=4k^4+12k^2+4k-3\).

Ta cần tìm số tự nhiên \(k\)để \(\Delta\)là số chính phương. 

Ta có: \(4k^4+12k^2+4k-3>4k^4+8k^2+4=\left(2k^2+2\right)^2\)

\(4k^4+12k^2+4k-3< 4k^4+16k^2+16=\left(2k^2+4\right)^2\)

Theo nguyên lí kẹp suy ra \(4k^4+12k^2+4k-3=\left(2k^2+3\right)^2\)

\(\Leftrightarrow4k-3=9\Leftrightarrow k=3\).

Với \(k=3\): \(a^2-19a-20=0\Rightarrow a=20\Rightarrow p=127\).

Vậy \(p\in\left\{2,127\right\}\).

bài kia dẽ mà lm bài này cho vui

Câu a =13 

Câu b =2 con câu c lam tuong tu 

tại sao caí bài này  ko làm đcj

1.Với  a = 2 ta có 2a + 1 = 5 không thích hợp

Với a   ≠ 2  do a là số nguyên tố nên a lẽ

Vậy 2a + 1 là lập phương của một số lẽ nghĩa là

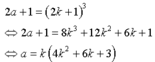
Từ đó k là ước của a. Do k là số nguyên tố nên k = 1 hoặc k = a

-Nếu k = 1 thì 2a + 1 = (2.1 + 1)³ suy ra a = 13 thớch hợp

-   Nếu a = k từ a = a(4a² + 6a + 3) do a là nguyên tố nên suy ra

 1 = 4a² + 6a + 3  không có số nguyên tố a nào thoả món phương trỡnh này  Vì vế phải luụn lớn hơn 1

Vậy a = 13

2.Giả sử  

13 và p là các số nguyên tố , mà n – 1 > 1 và n² + n + 1 > 1

Nên n – 1 = 13 hoặc  n – 1 = p

-    Với n – 1 =13 thì n = 14 khi đó 13p = n³ – 1 = 2743 suy ta p = 211 là số nguyên tố

- Với n – 1 = p thi n² + n + 1 = 13 suy ra n = 3 . Khi đó p = 2 là số nguyên tố

 Vậy  p = 2, p = 211 thì 13p + 1  là lập phương của một số tự nhiên

Đặt \(13p+1=n^3\left(n\in N\right)\)

\(\Leftrightarrow13p=n^3-1\)

\(\Leftrightarrow13p=\left(n-1\right)\left(n^2+n+1\right)\)

Trường hợp 1: \(n-1=13\forall n^2+n+1=p\)

\(\Leftrightarrow n=14\)

hay \(p=14^2+14+1=196+14+1=211\)(nhận)

Trường hợp 2: \(n-1=p\forall n^2+n+1=p\)

\(\Leftrightarrow n^2+2=13-p\)

\(\Leftrightarrow\left(p+1\right)^2=11-p\)

\(\Leftrightarrow p=2\)(nhận)

Vậy: \(p\in\left\{2;211\right\}\)