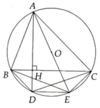
a, HS tự chứng minh

b, Ta chứng minh được  B E ⏜ = C D ⏜  từ đó suy ra BE = CD và tứ giác BDEC là hình thang cân 

Vì góc AED chắn nửa đường tròn tâm O ( AD )

=> \(\widehat{AED}=90^0\)

=> AE \(\perp\)AD hay AH \(\perp\)ED

Mà AH \(\perp\)BC 

=> ED // BC 

Vì góc ACD chắn nửa đường tròn => \(\widehat{ACD}=90^0\)

Ta có : \(\widehat{BEA}=\widehat{BCA}\)

Mặt khác : \(\widehat{BEA}+\widehat{EBC}=90^0;\widehat{BCA}+\widehat{BCD}=90^0\)

=> \(\widehat{EBC}=\widehat{BCD}\)

Xét hình thang BCDE ( ED // BC ) có :

\(\widehat{EBC}=\widehat{BCD}\)(hai góc cùng kề cạnh BC )

=> BCDE là hình thang cân

a: AM là phân giác của góc BAC
=>BM=CM

mà OB=OC

nên OM là trung trực của BC

=>OM vuông góc BC

b: Xét ΔHBA vuông tại H và ΔCDA vuông tại C có

góc HBA=góc CDA

=>ΔHBA đồng dạng với ΔCDA

=>góc BAH=góc DAC

=>góc IAM=góc DAM

=>AM là phân giác của góc IAD

c: AM là phân giác của góc IAD

nên sđ cung IM=sđ cung MD

=>IM=MD

=>OM là trung trực của ID

=>OM vuông góc ID

=>ID//BC

a) Từ O kẻ OM vuông góc với AD

Khi đó theo tính chất của đường kính và dây cung thì M là trung điểm AD

Lại có O là trung điểm AE => MO là đường trung bình của tam giác ADE

=> MO // DE , lại có MO // BC (cùng vuông góc với AD)

=> DE // BC

b) Tứ giác ABDC nột tiếp đường tròn (O) 

=> \(\widehat{ADB}=\widehat{BCA}\Leftrightarrow90^0-\widehat{ADB}=90^0-\widehat{BCA}\Rightarrow\widehat{CBD}=\widehat{ECB}\)

Lại có từ phần a, BED là hình thang vì có BC // DE

=> BCED là hình thang cân

a, Xét ΔADE nội tiếp đường tròn đường kính AE

=> AD ⊥ DE (1)

LẠi có AH ⊥ BC = > AD ⊥ BC (2)

Từ (1) và (2) => DE // BC ( cùng vuông góc với AD) (*)

b,  Ta có: Tứ giác ABDC nội tiếp

=> $\widehat{ADB}$= $\widehat{ACB}$

Lại có : $\widehat{CBD}$ + $\widehat{ADB}$ = $\widehat{ACB}$  + $\widehat{ECB}$ ( cùng bằng 90 độ)

=> $\widehat{CBD}$ = $\widehat{ECB}$ (**)

Từ (*) và (**) => BCED là hình thang cân

a) Xét (O) có : AE đường kính (GT)  và D ϵ (O) ⇒ Δ ADC vuông tại D

⇒ AD vuông góc với DE tại D. Mà BC vuông góc với AD tại H (GT) 

⇒ BC // DE ( theo định lí từ vuông góc đên song song )

b) CM dễ dàng △ AEC vuông tại C.

Xét (O) có : góc DBC = góc DAC ( vì 2 góc nội tiếp cùng chắn cung CD ) (1)

Mà góc DAC + góc ACB = 90 độ ( △AHC vuông tại H )

      góc BCE + góc ACB = 90 độ  ( △AEC vuông tại C )

⇒ góc DAC = góc BCE (2)

Từ (1) và (2) ⇒ góc DBC = góc BCE. 

Xét hình thang BCED (vì BC // ED) có ; góc DBC = góc BCE (cmt)

⇒ BCED là hình thang cân,

a) ta có: \(OD=OE=OA=\frac{1}{2}AE\)( bán kính đường tròn)

mà \(D\in\left(O;R\right)\)( giả thiết \(AH\)cắt \(\left(O;R\right)\)tại \(D\))

xét \(\Delta ADE\) có \(OD\) \(=\frac{1}{2}AE\) 

\(\Rightarrow OD\) là đường trung tuyến ứng với cạnh  \(AE\)

\(\Rightarrow\Delta ADE\) là \(\Delta\)vuông tại \(D\)

\(\Rightarrow AE\) là cạnh huyền trong tam giác vuông

ta cũng có \(O\)nằm giữa \(A,E\)( tâm đường tròn )

\(\Rightarrow A,O,E\) thẳng hàng