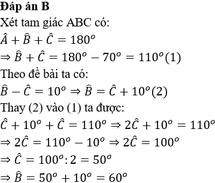Cho tam giác ABC có A=70o , B-C=20o. Tính B và C.

Những câu hỏi liên quan
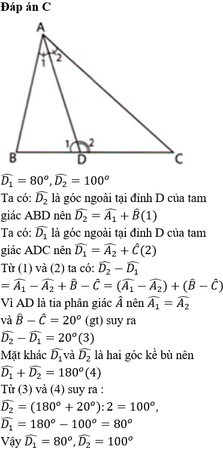
Cho tam giác ABC có ∠A =100o,∠B -∠C =20o. Tính ∠B và∠ C
Trong ΔABC, ta có:
∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
⇒ ∠B + ∠C = 180o - ∠A = 180o – 100o = 80o (1).
Theo giả thiết ta có: ∠B -∠C = 20o (2)
Từ (1) và (2) suy ra: 2∠B = 100o ⇒ ∠B = 50o
Vậy: ∠C = 80o - 50o = 30o
Đúng 0
Bình luận (0)
Có: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ b b) Chứng minh: Tính số đo D1̂ c) Chứng minh: IC là đường trung trực của đoạn thẳng AB.
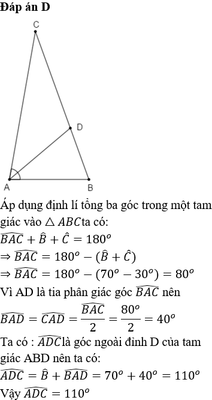
Cho tam giác ABC có
B
^
70
o
,
C
^
30
o
. Tia phân giác của góc A cắt cạnh BC tại D. Tính
A
D
C
^
A. 100
°
B. 120
°
C. 130
°
D. 110
°
Đọc tiếp
Cho tam giác ABC có B ^ = 70 o , C ^ = 30 o . Tia phân giác của góc A cắt cạnh BC tại D. Tính A D C ^
A. 100 °
B. 120 °
C. 130 °
D. 110 °
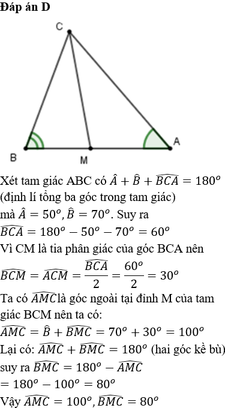
Cho tam giác ABC có
A
^
50
o
,
B
^
70
o
. Tia phân giác của góc C cắt cạnh AB tại M. Tính
A
M
C
^
,
B
M
C
^
A. ...
Đọc tiếp
Cho tam giác ABC có A ^ = 50 o , B ^ = 70 o . Tia phân giác của góc C cắt cạnh AB tại M. Tính A M C ^ , B M C ^
A. A M C ^ = 120 ° , B M C ^ = 60 °
B. A M C ^ = 80 ° , B M C ^ = 100 °
C. A M C ^ = 110 ° , B M C ^ = 70 °
D. A M C ^ = 100 ° , B M C ^ = 80 °
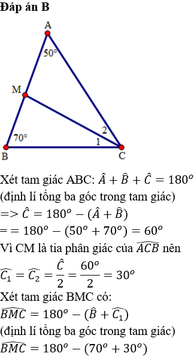
Cho tam giác ABC có
A
^
50
o
,
B
^
70
o
. Tia phân giác của góc C cắt AB tại M. Tính số đo góc BMC A. 60
°
B. 80
°
C. 90
°
D. 100
°
Đọc tiếp
Cho tam giác ABC có A ^ = 50 o , B ^ = 70 o . Tia phân giác của góc C cắt AB tại M. Tính số đo góc BMC
A. 60 °
B. 80 °
C. 90 °
D. 100 °
Tam giác ABC có
A
^
70
o
,
B
^
-
C
^
10
o
. Số đo góc B và góc C lần lượt là: A.
B
^
70
°
,
C
^
40
°
B.
B
^
60...
Đọc tiếp
Tam giác ABC có A ^ = 70 o , B ^ - C ^ = 10 o . Số đo góc B và góc C lần lượt là:
A. B ^ = 70 ° , C ^ = 40 °
B. B ^ = 60 ° , C ^ = 50 °
C. B ^ = 70 ° , C ^ = 60 °
D. B ^ = 50 ° , C ^ = 60 °
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo
A
D
C
^
biết
B
^
-
C
^
20
o
A. 80
°
B. 110
°
C. 100
°
D. 105
°
Đọc tiếp
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo A D C ^ biết B ^ - C ^ = 20 o
A. 80 °
B. 110 °
C. 100 °
D. 105 °
Tam giác ABC có
A
^
40
o
;
B
^
-
C
^
20
o
. Trên tia đối của tia AC lấy điểm E sao cho AEAB. Tính số đo góc CBE A. 80
°
B. 100
°
C. 90
°
D. 120
°
Đọc tiếp
Tam giác ABC có A ^ = 40 o ; B ^ - C ^ = 20 o . Trên tia đối của tia AC lấy điểm E sao cho AE=AB. Tính số đo góc CBE
A. 80 °
B. 100 °
C. 90 °
D. 120 °
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(ADH)
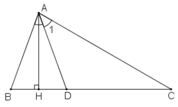
Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o
Đúng 0
Bình luận (0)