Một vật dao động điều hòa theo phương trình x=4cos(20pi.t-pi/2)(cm). Thời gian ngắn nhất để vật đi từ vị trí có li độ x1=2cm đến li độ x2=4cm bằng

Những câu hỏi liên quan
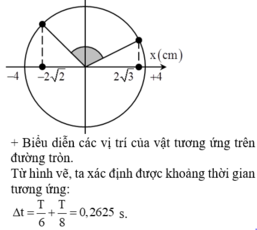
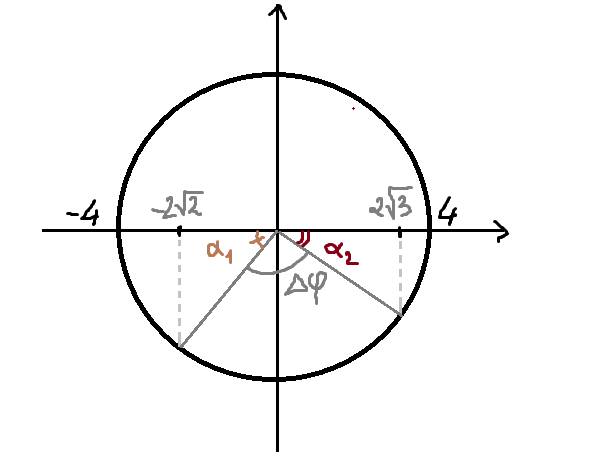
Vật dao động điều hòa theo phương trình : x = 4cos(π.t - π/6) cm .Thời gian ngắn nhất vật đi từ vị trí có li độ x1=−2√2 cm đến vị trí có li độ x2 = 2√3 cm theo chiều âm là :
Ta có : \(A=4cm\)
\(cos\alpha_1=\dfrac{-2\sqrt{2}}{4}=-\dfrac{\sqrt{2}}{2}\Rightarrow\alpha_1=\dfrac{3\pi}{4}rad\)
\(cos\alpha_2=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\Rightarrow\alpha_2=\dfrac{\pi}{6}rad\)
\(\Delta\varphi=\left(\dfrac{\pi}{2}-\dfrac{3\pi}{4}\right)+\left(\dfrac{\pi}{2}-\dfrac{\pi}{6}\right)=\dfrac{\pi}{12}rad\)
Có : \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s\)
\(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{\pi}{12}}{2\pi}.2=\dfrac{1}{12}s\)
Vậy ...
Hình ảnh biểu diễn :
Đúng 2
Bình luận (0)
Một vật dao động điều hoà theo phương trình x 4cos(8πt - 2π/3) (cm). Tốc độ trung bình của vật khi đi từ vị trí có li độ x1 -2√3 cm theo chiều dương đến vị trí có li độ x2 2√3 cm theo chiều dương bằng: A. 4.8√3 cm/s. B. 48√3 m/s. C. 48√2 cm/s. D. 48√3 cm/s.
Đọc tiếp
Một vật dao động điều hoà theo phương trình x = 4cos(8πt - 2π/3) (cm). Tốc độ trung bình của vật khi đi từ vị trí có li độ x1 = -2√3 cm theo chiều dương đến vị trí có li độ x2 = 2√3 cm theo chiều dương bằng:
A. 4.8√3 cm/s.
B. 48√3 m/s.
C. 48√2 cm/s.
D. 48√3 cm/s.
Chọn D
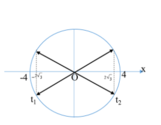
+ T = 2 π w = 2 π 8 π = 0 , 25 s
+ Quãng đường vật đi được là: S = 2 3 + 2 3 = 4 3 cm.
+ Sử dụng vòng tròn ta có thời gian vật đi từ
x1 = - A 3 2 đến x2 = A 3 2 là:
t = t - A 3 / 2 → O + t A 3 / 2 → O = T 6 + T 6 = T 3 = 1 12 s .
+ Tốc độ trung bình: vtb = S: t = 48 3 cm/s.
Đúng 0
Bình luận (0)
Một chất điểm dao động điều hòa với biên độ 4cm, chu kì 0,9s. Tìm thời gian ngắn nhất để vật đi từ vị trí có li độ 2 3 cm đến vị trí có li độ - 2 2 cm theo chiều âm.
A. 0,375s
B. 0,2625 s
C. 0,225 s
D. 0,5252 s
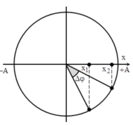
Một vật dao động điều hòa với phương trình x=5cos(4pi—pi/2)(cm). Xác định thời gian ngắn nhất để vật đi từ vị trí có li độ x1=2,5(cm) đến x2=—2,5(cm).
A. 1/6(s)
B. 1/5(s)
C. 1/20(s)
D.1/12(s)
Bạn vẽ véc tơ quay ra để tìm nhé.
Dao động từ -2,5cm đến 2,5cm ứng với véc tơ quay từ M đến N
Góc quay là: \(60^0\)
Thời gian: \(t=\dfrac{60}{360}T=\dfrac{1}{6}.\dfrac{2\pi}{4\pi}=\dfrac{1}{12}s\)
Đúng 0
Bình luận (0)
giúp em với ạ, em cảm ơn nhiều!Câu 1. Một vật dao động điều hòa với phương trình x 4cos(4πt –) cma) xác định thời gian ngắn nhất vật đi từ vị trí có li độ x 2 về vị trí cân bằng; vị trí x2√3 về vị trí biên.b) xác định thời gian ngắn nhất vật đi từ vị trí x 2 đến vị trí x -2.c) xác định vận tốc, gia tốc, ly độ khi vật dao động sau thời gian 1s.d) xác định li độ và gia tốc biết rằng khi đó vật đang chuyển động với tốc độ 18 π đang chuyển động theo chiều dương.e) Xác định thời điểm vật qua vị trí...
Đọc tiếp
giúp em với ạ, em cảm ơn nhiều!
Câu 1. Một vật dao động điều hòa với phương trình x = 4cos(4πt –) cm
a) xác định thời gian ngắn nhất vật đi từ vị trí có li độ x = 2 về vị trí cân bằng; vị trí x=2√3 về vị trí biên.
b) xác định thời gian ngắn nhất vật đi từ vị trí x= 2 đến vị trí x= -2.
c) xác định vận tốc, gia tốc, ly độ khi vật dao động sau thời gian 1s.
d) xác định li độ và gia tốc biết rằng khi đó vật đang chuyển động với tốc độ 18 π đang chuyển động theo chiều dương.
e) Xác định thời điểm vật qua vị trí x = 2cm theo chiều dương lần thứ 5 kể từ thời điểm ban đầu.
f) xác định thời điểm vật qua vị trí x = 2√2 cm theo chiều dương lần thứ 2 kể từ thời điểm t= 2 s.
Một vật dao động với phương trình
x
6
cos
4
π
t
+
6
π
(
c
m
)
(t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 3cm theo chiều dương đến vị trí có li độ
−
3
3
c
m
là A. 7/24 s B. 1/4 s C. 5/24 s...
Đọc tiếp
Một vật dao động với phương trình x = 6 cos 4 π t + 6 π ( c m ) (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 3cm theo chiều dương đến vị trí có li độ − 3 3 c m là
A. 7/24 s
B. 1/4 s
C. 5/24 s
D. 1/8 s
Chọn đáp án A
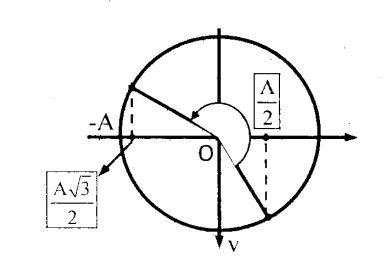
x 1 = 3 = A 2 → x 2 = − 3 2 = − A 3 2
Từ VTLG ta thu được thời gian cần tìm là:
Δ t = T 2 + T 12 → T = 0 , 5 s Δ t = 7 24 s
Đúng 0
Bình luận (0)
Một vật dao động điều hòa với chu kì T 6 s, khoảng thời gian ngắn để vật đi từ vị trí có li độ
x
1
A
2
đến vị trí có li độ
x
2
+
A
3
2
là: A. 0,25 s B. 0,15 s. C. 0,5 s. D. 0,4 s.
Đọc tiếp
Một vật dao động điều hòa với chu kì T = 6 s, khoảng thời gian ngắn để vật đi từ vị trí có li độ x 1 = A 2 đến vị trí có li độ x 2 = + A 3 2 là:
A. 0,25 s
B. 0,15 s.
C. 0,5 s.
D. 0,4 s.
Một vật dao động với phương trình x 6cos(4πt + π/6 ) (cm) (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 3 cm theo chiều dương đến vị trí có li độ
−
3
3
cm là A. 7 /24 s B. 1/ 4 s C. 5 /24 s D.1/ 8 s
Đọc tiếp
Một vật dao động với phương trình x = 6cos(4πt + π/6 ) (cm) (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 3 cm theo chiều dương đến vị trí có li độ − 3 3 cm là
A. 7 /24 s
B. 1/ 4 s
C. 5 /24 s
D.1/ 8 s
Một vật dao động với phương trình x 6cos(4πt + π 6 ) (cm) (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 3 cm theo chiều dương đến vị trí có li độ −3√3 cm là A. 7 /24 s. B. 1/ 4 s. C. 5 /24 s. D. 1/ 8 s.
Đọc tiếp
Một vật dao động với phương trình x = 6cos(4πt + π 6 ) (cm) (t tính bằng s). Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ 3 cm theo chiều dương đến vị trí có li độ −3√3 cm là
A. 7 /24 s.
B. 1/ 4 s.
C. 5 /24 s.
D. 1/ 8 s.