xác định m để hàm số y=x3-3x2+3mx+3m+4:
a. không có cực trị
b. có cực đại và cực biểu
Cho hàm số y = x 3 - 3 x 2 - m . Tìm m để hàm số có giá trị cực đại và giá trị cực tiểu trái dấu nhau.
A. m > 0 hoặc m < - 4
B. 0 < m < 4
C. - 4 < m < 0
D. m > 4 hoặc m < 0
Cho hàm số y = x 3 − 3 x 2 − m . Tìm m để hàm số có giá trị cực đại và giá trị cực tiểu trái dấu nhau.
A. 0 < m < 4
B. m > 4 hoặc m < 0
C. m > 0 hoặc m < - 4
D. − 4 < m < 0
Cho hàm số y = x3 + 3x2 + mx + m - 2 (m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.
A.![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Chọn B
PT hoành đồ giao điểm của (C) và trục hoành:
x3 + 3x2 + mx + m - 2 = 0 (1)
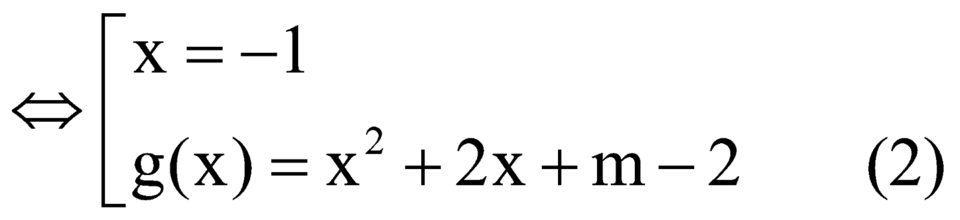
(Cm) có 2 điểm cực trị nằm về hai phía đối với trục Ox
![]() PT (1) có 3 nghiệm phân biệt
PT (1) có 3 nghiệm phân biệt
![]() (2) có 2 nghiêm phân biệt khác -1
(2) có 2 nghiêm phân biệt khác -1
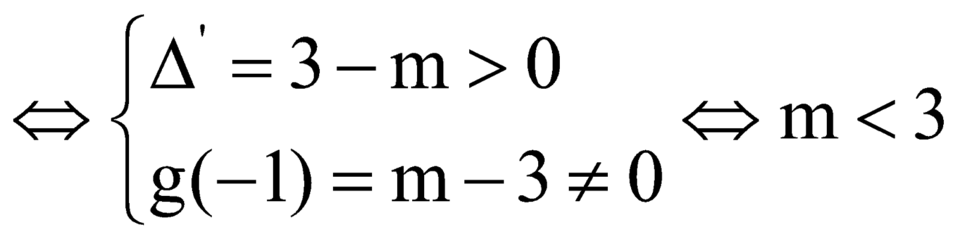
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Đáp án: C.
Để có cực đại, cực tiểu, phương trình y' = 3 x 2 + 2mx = 0 phải có hai nghiệm phân biệt.
Phương trình y' = x(3x + 2m) = 0 có hai nghiệm phân biệt x1 = 0, x2 = -2m/3 khi và chỉ khi x ≠ 0.
Xác định giá trị của tham số m để hàm số y = x 3 + m x 2 - 3 có cực đại và cực tiểu.
A. m = 3; B. m > 0;
C. m ≠ 0; D. m < 0.
Đáp án: C.
Để có cực đại, cực tiểu, phương trình y' = 3 x 2 + 2mx = 0 phải có hai nghiệm phân biệt.
Phương trình y' = x(3x + 2m) = 0 có hai nghiệm phân biệt x 1 = 0, x 2 = -2m/3 khi và chỉ khi x ≠ 0.
Cho hàm số:
y = x 3 + m + 3 x 2 + 1 - m (m là tham số)
có đồ thị C m .
Xác định m để hàm số có điểm cực đại là x = -1.
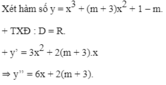
+ Hàm số có điểm cực đại là x = -1
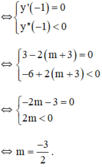
Vậy với 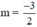 thì hàm số có điểm cực đại là x = -1.
thì hàm số có điểm cực đại là x = -1.
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
∆ ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
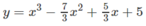
Ta có:
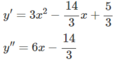
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y CT = y(1) = (16/3).
Xác định m để hàm số: y = x 3 − m x 2 + (m – 2/3)x + 5 có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: y′ = 3 x 2 − 2mx + (m – 2/3)
Δ’ > 0 khi m < 1 hoặc m > 2 (∗)
Để hàm số có cực trị tại x = 1 thì
y′(1) = 3 − 2m + m – 2/3 = 0 ⇔ m = 7/3, thỏa mãn điều kiện (∗)
Với m = 7/3 thì hàm số đã cho trở thành:
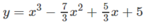
Ta có:
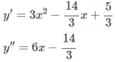
Vì y′′(1) = 6 – (14/3) > 0 nên hàm số đạt cực tiểu tại x = 1 và y C T = y(1) = (16/3).
Tìm tất cả các giá trị thực của tham số m để hàm số y= x3-3x2+3mx+1 có các điểm cực trị nhỏ hơn 2
A. -1> m
B. m< 1
C. m> 0
D. 0< m< 1
Ta có y’= 3x2-6x+3m
Yêu cầu bài toán khi y’=0 có hai nghiệm phân biệt x1<x2<2
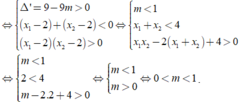
Chọn D.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = - x 3 + 3 x 2 + 3 ( m 2 - 1 ) x - 3 m 2 - 1 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A. 0
B. 1
C. 2
D. 3
+ Đạo hàm y’ = -3x2+ 6x+ 3( m2-1) = -3( x2- 2x-m2+1).
Đặt g( x) = x2- 2x-m2+1 là tam thức bậc hai có ∆ ' = m 2 .
+ Do đó hàm số đã cho có cực đại cực tiểu khi và chỉ khi y’ =0 có hai nghiệm phân biệt hay g(x) =0 có hai nghiệm phân biệt
⇔ ∆ ' > 0 ⇔ m ≠ 0 . (1)
+ Khi đó y’ có các nghiệm là: 1±m .
Tọa độ các điểm cực trị của đồ thị hàm số là A( 1-m ; -2-2m3) và B( 1+m ; -2+ 2m3).
Ta có:
O A → ( 1 - m ; - 2 - 2 m 3 ) ⇒ O A 2 = ( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 . O B → ( 1 + m ; - 2 + 2 m 3 ) ⇒ O B 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 .
Để A và B cách đều gốc tọa độ khi và chỉ khi OA= O B hay OA2= OB2
( 1 - m ) 2 + 4 ( 1 + m 3 ) 2 = ( 1 + m ) 2 + 4 ( 1 - m 3 ) 2 ⇔ - 4 m + 16 m 3 = 0
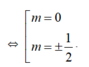
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
Vậy không có giá trị nguyên nào của m thỏa mãn yêu cầu bài toán.
Chọn A.