Tìm một số biết rằng ba lần bình phương của nó đúng bằng 2 lần bình phương của số ấy.

Những câu hỏi liên quan
BÀi 3 : tìm một số biết rằng ba lần bình phương của nó đúng bằng hai lần lập phương của số ấy
Trả lời :
\(2x^3-3x^2=0\)
\(\Leftrightarrow x^2\left(2x-3\right)=0\)
\(\Leftrightarrow x=0\text{ or }x=\frac{3}{2}\)
~HT~
Tìm một số khác 0 biết rằng bình phương của nó bằng 5 lần lập phương của số ấy A. 5 B.
1
5
C.
1
25
D.
-
1
5
Đọc tiếp
Tìm một số khác 0 biết rằng bình phương của nó bằng 5 lần lập phương của số ấy
A. 5
B. 1 5
C. 1 25
D. - 1 5
Gọi số cần tìm là x (x ≠ 0). Theo đề bài ta có
x 2 = 5 x 3 ⇔ 5 x 3 – x 2 = 0 ⇔ x 2 . 5 x – x 2 = 0 ⇔ x 2 ( 5 x – 1 ) = 0
ó x 2 = 0 5 x - 1 = 0 ó x = 0 l 5 x = 1 => x = 1 5 ™
Vậy số cần tìm là 1 5
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Bài nèy còn dễ hơn : Tìm 1 số biết rằng 3 lần bình phương của nó đúng bằng 2 lần lập phương của nó .
tìm một số biết rằng bình phương của nó bằng 9 lần số đó
Tìm một số có hai chữ số biết rằng số đó bằng lập phương của một số tự nhiên và tổng các chữ số của nó bằng bình phương của số tự nhiên ấy
Gọi số có 2 chữ số là ab. 9 ≥ a ≥ 1 , 9 ≥ b ≥ 0 , a,b thuộc N.
Theo đề ta có :
( a + b ) ³ = ( 10 a + b ) ²
< = >a + b = [ 1 + 9 a / ( a + b) ] ²
=> a + b là số chính phương và 9a chia hết cho ( a + b)
=> a + b \(\in\){ 1 ; 4 ; 9 ; 16 } và 9a chia hết cho ( a + b )
a + b = 1 => 10 a + b = 1 (loại)
a + b = 4 => 10 a + b = 8 (loại)
a + b = 9 => 10 a + b = 27 => a = 2 và b = 7 (nhận)
a + b = 16=> 10 a + b = 64 => a = 6 và b = 4 (loại)
Vậy số cần tìm là 27
Tìm một số tự nhiên có hai chữ số biết rằng số đó bằng lập phương của một số tự nhiên và tổng các chữ số của nó bằng bình phương của số tự nhiên ấy
Tìm 1 số có 2 chữ số biết 3 lần số đó bằng bình phương tổng các chữ số của nó và số đó bằng 4 lần tổng các chữ số của nó
Tìm một cấp số cộng tăng, biết rằng tổng ba số hạng đầu của nó bằng 27 và tổng các bình phương của chúng bằng 275.
Gọi công sai của cấp số cộng là d; số hạng đầu là u1 = x - d, u2 = x, u3 = x + d.
CSC tăng nên d > 0.
Theo giả thiết, ta có hệ:
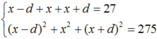
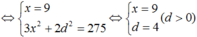
Vậy cấp số cộng cần tìm là : 5, 9, 13 .
Đúng 0
Bình luận (0)
Cho hai số tự nhiên biết rằng hai lần số thứ nhất hơn ba lần số thứ hai là 9 và hiệu các bình phương của chúng bằng 119. Tìm số lớn hơn.
A. 12
B. 13
C. 32
D. 33
Đáp án A
Gọi số thứ nhất là a; a ∈ N, số thứ hai là b; b ∈ N Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
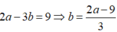
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
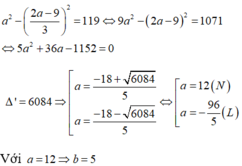
Vậy số lớn hơn là 12.
Đúng 0
Bình luận (0)














