Tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của các tam giác ABC, AHB, AHC ?

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC.
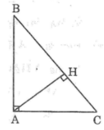
*Tam giác ABC có ∠(BAC) = 90o
Vì CA là đường cao xuất phát từ đỉnh C; BA là đường cao xuất phát từ đỉnh B
Và hai đường cao này cắt nhau tại A nên A là trực tâm của ΔABC.
*Tam giác AHB có ∠(AHB) = 90o
Vì AH là đường cao xuất phát từ đỉnh A, BH là đường cao xuất phát từ đỉnh B và giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHB.
*Tam giác AHC có ∠(AHC) = 90o
Vì AH là đường cao xuất phát từ đỉnh A, CH là đường cao xuất phát từ đỉnh C và giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHC.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A ,đường cao AH. Tìm trực tam của các tam giác ABC, AHB, AHC.
Cho tam giác ABC Các đường cao AK BN cm điểm M là trực tâm của tam giác Tìm trực tâm của tam giác bhc tam giác ahc tam giác ahb
Xét ΔACB có
AK,BN là các đườg cao
AK cắt BN tại M
=>M là trực tâm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, J, K lần lượt là tâm đường tròn nội tiếp của tam giác ABC, tam giác AHB, tam giác AHC. Chứng minh AI vuông góc JK.
CHO TAM GIÁC CÓ GÓC A ĐƯỜNG CAO AH. HÃY XÁC ĐỊNH TRỰC TÂM CUẢ TAM GIÁC ABC, TAM GIÁC AHB, TAM GIÁC AHC
cho tam giác ABC vuông tại A, đường cao AH. Gọi I,J,K lần lượt là tâm đường tròn nội tiếp tam giác ABC, AHB, AHC. C/M: AI vuông góc JK .
2) Cho tam giác ABC vuông tại A, có đường cao AH, gọi I,J, K lần lượt là tâm đường tròn nội tiếp các tam giác ABC, AHB, AHC.
a) C/m AI vuông góc với JK
b) C/m tứ giác BJKC nội tiếp đuợc đường tròn
Cho tam giác ABC vuông tại A , đường cao AH , biết HB = 3,6cmvaf AC = 8cm . Tính diện tích các tam giác ABC , AHB , AHC . Kẻ các đường trung tuyến AM và đường phân giác AD . Tính diện tích tam giác AHM và tam giác AHD
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết chu vi tam giác AHB là 30 cm, chu vi tam giác AHC là 40 cm. Tính chu vi tam giác ABC.
Ta có hình vẽ
Ta có : ΔABH + ΔACH = ΔABC
Hay: 30 + 40 = ΔABC
=> ΔABC = 70 cm
mk k bít dug hay sai đâu đó...
mk chỉ thử lm thui ak^^^
Đúng 0
Bình luận (2)















