Cho hình bs 15 (hai đường thẳng FE, GH song song với nhau, hai đường thẳng FG, EH song song với nhau).
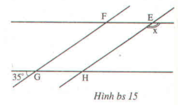
Khi đó, số đo của góc x bằng
(A) 35o;
(B) 145o;
(C) 155o;
(D) không tính được
Cho hình bs 4 (hai đường thẳng a và b song song với nhau). Cho biết số đo của mỗi góc: ∠(D1 ) ; ∠(D2 ) ; ∠(D3 ) ; ∠(D3và giải thích cách tìm.
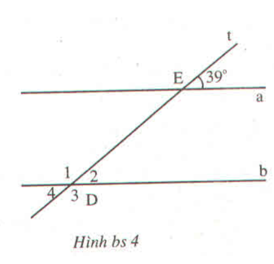
∠D2 = 39° vì là góc đồng vị với ∠E = 39°.
∠D4 = 39° vì là góc đối đỉnh với ∠D2.
∠D3 = 141° vì bù với góc ∠D4.
∠D1 = 141° vì là góc đối đỉnh với ∠D3.
Cho hình bs 4 (hai đường thẳng a và b song song với nhau). Cho biết số đo của mỗi góc: ∠(D1 ) ; ∠(D2 ) ; ∠(D3 ) ; ∠(D3và giải thích cách tìm.
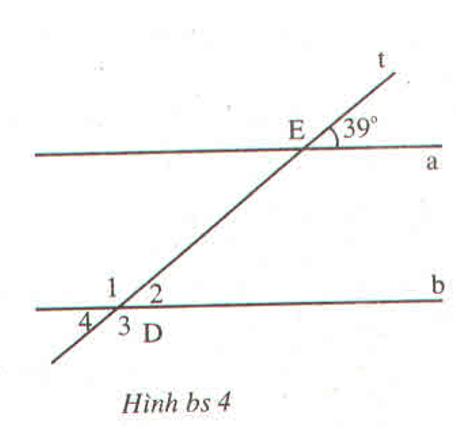
∠D2 = 39° vì là góc đồng vị với ∠E
∠D4 = 39° vì là góc đối đỉnh với ∠D2
∠D3 = 141° vì bù với góc ∠D4
∠D1 = 141° vì là góc đối đỉnh với ∠D3
Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau.
Chứng minh rằng:
a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.
b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.
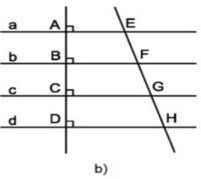
a) Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD
⇒ B là trung điểm của AC; C là trung điểm của BD
- Hình thang AEGC (AE // GC) có B là trung điểm của AC và BF song song hai cạnh đáy
⇒ F là trung điểm EG (định lí đường trung bình của hình thang)
⇒ EF = FG
- Chứng minh tương tự ⇒ G là trung điểm FH
⇒ FG = GH
Vậy EF = FG = GH
Cho hình bs 8 (các đường thẳng Er, Dp và Fq song song với nhau). Khi đó, hai đường thẳng DE và DF có vuông góc với nhau không ? Vì sao ?
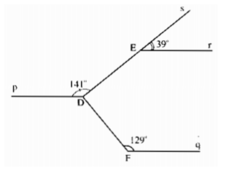
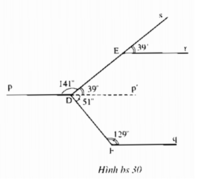
+) Ta có hai đường thẳng DE và DF cắt nhau tại D.
+) Kẻ tia Dp’ là tia đối của tia Dp.
+) Do Er // Dp nên Er // Dp’
Suy ra
+) Ta có tia Dp’ nằm giữa hai tia DF và tia DE nên:
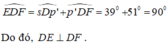
Cho hình bs 10 (hai đường thẳng a, b song song với nhau và hai đường thẳng c, d song song với nhau; Dm, Cp, Bq và An tương ứng là các tia phân giác).
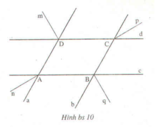
Chứng minh: An vuông góc với Bq.
Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
\(Cho hình bs 8 (các đường thẳng Er, Dp và Fq song song với nhau). Khi đó hai đường thẳng DE và DF có vuông góc với nhau không ? Vì sao ? \)
Cho trước 4 đường thẳng phân biệt m, n, p và q
a) Biết m song song với n thêm vào đó p vuông góc với m còn q vuông góc với n. Khi đó hai đường thẳng p và q có song song với nhau không ?
b) Biết m vuông góc với n thêm vào đó n vuông góc với p còn p vuông góc với q. Khi đó hai đường thẳng m và q có vuông góc với nhau không ?
c) Biết m vuông góc với n, p song song với m và q song song với n. Khi đó, hai đường thẳng p và q vuông góc với nhau hay song song với nhau ?
d) Biết m vuông góc với n, p vuông góc với m và q vuông góc với n. Khi đó hai đường thẳng p và q vuông góc với nhau hay song song với nhau ?
a) p có song song với q
b) m vuông góc với q
c) Hai đường thẳng p và q vuông góc với nhau
d) Hai đường thẳng p và q vuông góc với nhau
cho hình bs 10 (hai đường thẳng ab song song với nhau và hai đường thẳng c,d song song với nhau ; Dm,Cp,Bq và An tương ứng là các tia phân giác). a) Chứng minh : An // Cp và Dm // Bq. b) Chứng minh : An vuông góc với Bq
